dùng diện tích để chứng tỏ (a+b) 2 = a2 + 2ab + b2
dùng diện tích để chứng tỏ (a-b)2 = a2 - 2ab + b2
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


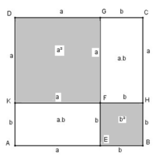
Dựng hình vuông ABCD có cạnh bằng a
Trên cạnh AB lấy điểm E sao cho BE = b
Từ E dựng đường thẳng song song BC cắt CD tại G
Ta có: CG = b, CE = ( a – b ), GD = ( a – b )
Trên cạnh AD lấy điểm K sao cho AK = b
Từ K kẻ đường thẳng song song với AB cắt BC tại H và cắt EG tại F
Ta có: KD = ( a – b ), BH = b
Hình vuông ABCD có diện tích bằng a 2
Hình vuông DKFG có diện tích bằng a - b 2
Hình chữ nhật AEFK có diện tích bằng ( a – b ) b
Hình vuông EBHF có diện tích bằng b 2
Hình chữ nhật HCGF có diện tích bằng ( a – b ).b
S A B C D = S D K F G + S A E F K = S E B H F + S H C G F
nên a - b 2 + a - b b + a - b b + b 2 = a 2
⇒ a - b 2 = a 2 - 2 a b + b 2

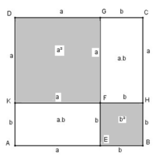
Dựng hình vuông ABCD có cạnh bằng (a + b )
Trên cạnh AB dựng điểm E sao cho AE = a, EB = b, trên cạnh BC dựng điểm H sao cho BH = b, HC = a, trên cạnh CD dựng điểm G sao cho CG = b, GD = a, trên cạnh DA dựng điểm K sao cho DK = a, KA = b, GE cắt KH tại F.
Ta có : diện tích hình vuông ABCD bằng a + b 2
Diện tích hình vuông DKFG bằng a 2
Diện tích hình chữ nhật AKFE bằng a.b
Diện tích hình vuông EBHF bằng b 2
Diện tích hình chữ nhật HCGF bằng a.b
S A B C D = S D K F G + S A K E F + S E B H F + S H C G F
Vậy ta có : a + b 2 = a 2 + 2 a b + b 2
dùng diện tích để chứng tỏ (a+b) 2 = a2 + 2ab + b2
dùng diện tích để chứng tỏ (a-b)2 = a2 - 2ab + b2

Bài 2.2 - Bài tập bổ sung Sách bài tập - trang 159 - Toán lớp 8 | Học trực tuyến

(a-b)^2=(a-b)(a-b)=a^2-ab-ab+b^2=a^2-2ba+b^2
(a-b)(a+b)=a^2+ab-ab-b^2=a^2-b^2
(a+3)^3=(a+b)^2*(a+b)
=(a^2+2ab+b^2)(a+b)
=a^3+a^2b+2a^2b+2ab^2+b^2a+b^3
=a^3+3a^2b+3ab^2+b^3
dùng nhân đa thức với đa thức
bạn kai nói đúng rồi đó nha