Gọi thời gian làm riêng hoàn thành công việc của người thứ nhất là x (ngày) với x>0

Thời gian làm riêng hoàn thành của hai là y ngày (y>0)

Do người 2 làm ít hơn người 1 là 6 ngày nên: \(x-y=6\)

Trong 1 ngày người thứ nhất làm được \(\dfrac{1}{x}\) phần công việc

Trong 1 ngày người thứ hai làm được \(\dfrac{1}{y}\) phần công việc

Do 2 người làm chung trong 4 ngày xong việc nên: \(4\left(\dfrac{1}{x}+\dfrac{1}{y}\right)=1\)

Ta có hệ: \(\left\{{}\begin{matrix}x-y=6\\\dfrac{4}{x}+\dfrac{4}{y}=1\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x=y+6\\\dfrac{4}{y+6}+\dfrac{4}{y}=1\end{matrix}\right.\)

\(\Rightarrow\left\{{}\begin{matrix}x=y+6\\4y+4\left(y+6\right)=y\left(y+6\right)\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}x=y+6\\y^2-2y-24=0\end{matrix}\right.\)

\(\Rightarrow\left\{{}\begin{matrix}x=12\\y=6\end{matrix}\right.\)

Gọi x (giờ) là thời gian đội I làm một mình xong công việc (x > 12)

Thời gian đội thứ II làm một mình xong công việc là: x – 7 (giờ)

Trong một giờ đội I làm được 1/x (công việc)

Trong một giờ đội II làm được 1/(x-7) (công việc)

Trong một giờ cả hai đội làm được 1/12 (công việc)

Theo bài ra ta có phương trình:

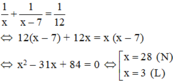
Vậy thời gian đội I làm xong công việc là 28 giờ, thời gian đội II làm xong công việc là: 28 – 7 = 21 (giờ)

Đáp án: C

đổi 2 giờ 40 phút=\(\dfrac{8}{3}\) giờ

gọi thời gian đội 1 và đội 2 làm riêng để hoàn thành công việc lần lượt là

x,y(x,y>\(\dfrac{8}{3}\) )

=>hệ pt: \(\left\{{}\begin{matrix}\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{\dfrac{8}{3}}=\dfrac{3}{8}\\y-x=4\end{matrix}\right.\) giải hệ pt trên ta được \(\left\{{}\begin{matrix}x=4\left(TM\right)\\y=8\left(TM\right)\end{matrix}\right.\)

vậy nếu làm riêng để hoàn thành công việc thì đội thứ nhất hết 4 giờ

đội thứ 2 hết 8 giờ

Bài giải:

Chiều rộng hình chữ nhật là:

        12 : 4 = 3 ( dm)

Chu vi mảnh tấm bìa đó  là:

        ( 12 + 3 ) x 2 = 30 ( dm)

                 Đáp số: 30dm.

Đề nghị bạn Hồ Trần Mạnh Quỳnh không trả lời linh tinh

Gọi x,y(h) lần lượt thời gian làm riêng xong cv của người 1 và 2(x,y>0)

Trong 1h người 1 làm được 1/x công việc

Trong 1h người 2 làm được 1/y công việc 

Trong 1h 2 người làm chung được 1/16 công việc 

Ta có pt1:  1/x   +   1/y  =   1/16

Trong 3h người 1 làm được 3/x công việc

Trong 6h người 2 làm được 6/y công việc

Ta có pt2:   3/x    +     6/y      =1/4

DONE

Hệ bạn tự giải nha

Lời giải. Phần công việc mà hai đội đã làm chung nhanh hơn so với đội thứ nhất là 12 giờ. Để hoàn thành công việc, đội hai làm nhanh hơn đội một là 18 giờ. Suy ra phần công việc mà đội hai đã làm chiếm 12/18 = 2/3 lượng công việc. Vậy, đội hai đã làm trong 12 × 2 3 = 8 giờ. Đáp số: 8 giờ. 

Gọi số sản phẩm tổ 1 được giao theo kế hoạch là x(sản phẩm), số sản phẩm tổ 2 được giao theo kế hoạch là y(sản phẩm)

(ĐIều kiện: \(x,y\in Z^+\))

Theo kế hoạch, hai đội được giao 2400 sản phẩm nên 

x+y=2400(1)

Số sản phẩm đội 1 làm được là x(1+15%)=1,15x(sản phẩm)

Số sản phẩm đội 2 làm được là:

y(1+12%)=1,12y(sản phẩm)

Thực tế hai đội làm được 2733 sản phẩm nên 1,15x+1,12y=2733(2)

Từ (1),(2) ta có hệ phương trình:

\(\left\{{}\begin{matrix}x+y=2400\\1,15x+1,12y=2733\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}1,15x+1,15y=2760\\1,15x+1,12y=2733\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}0,03y=27\\x+y=2400\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}y=900\\x=2400-900=1500\end{matrix}\right.\left(nhận\right)\)

vậy: Số sản phẩm được theo kế hoạch của đội 1 và đội 2 lần lượt là 1500 sản phẩm và 900 sản phẩm

goi thoi gian moi doi phai lam theo ke hoach la x( ngay,x>0)

thoi gian doi 1 da lam la x-2 (ngay)

thoi gian doi 2 da lam la x+2 ( ngay )

moi ngay doi 1 trong duoc $\frac{40}{x-2}$(ha)

moi ngay doi 2 trong duoc $\frac{90}{x+2}$(ha)

neu doi 1 lam xong x+2 ngay thi trong duoc $\frac{40}{x-2}\left(x+2\right)$(ha)

nếu đội 2 làm xong x-2 ngày thì trồng được

$\frac{90}{x+2}\left(x-2\right)\left(ha\right)$

theo de bai thi dien h rung trong duoc cua 2 doi la bang nhau nen ta co pt:

$\frac{40}{x-2}\left(x+2\right)=\frac{90}{\left(x+2\right)}\left(x-2\right)$

=> x=10 hoac x=2/5

x₂>2=> x=2/5 loai

Tham khảo 

Gọi thời gian đội thứ nhất và đội thứ hai cần để hoàn thành công việc đó lần lượt là a,ba,b
Từ đề bài, đội thứ nhất có 18 người , đội thứ hai có 15 người ( các công nhân làm việc với năng suất như nhau ) ⇒18a=15b⇒a15=b18⇒18a=15b⇒a15=b18
Áp dụng tính chất dãy tỉ số bằng nhau:

a15=b18=b−a18−15=63=2a15=b18=b-a18-15=63=2

Do đó:
a15=2→a=2.15=30a15=2→a=2.15=30
b18=2→b=2.18=36b18=2→b=2.18=36
Vậy thời gian đội thứ nhất và thứ hai cần để hoàn thành công việc lần lượt là 30giờ30giờ và 

nhìn ứ hiểu j