a)Có \(a^2+1\ge2a\) với mọi a; \(b^2+1\ge2b\) với mọi b

Cộng vế với vế \(\Rightarrow a^2+b^2+2\ge2\left(a+b\right)\)

Dấu = xảy ra <=> a=b=1

b) Áp dụng BĐT bunhiacopxki có:

\(\left(x+y\right)^2\le\left(1+1\right)\left(x^2+y^2\right)\Leftrightarrow\left(x+y\right)^2\le2\)

\(\Leftrightarrow-\sqrt{2}\le x+y\le\sqrt{2}\)

\(\Rightarrow\left(x+y\right)_{max}=\sqrt{2}\Leftrightarrow\left\{{}\begin{matrix}x+y=\sqrt{2}\\x=y\end{matrix}\right.\)\(\Leftrightarrow x=y=\dfrac{\sqrt{2}}{2}\)

\(\left(x+y\right)_{min}=-\sqrt{2}\Leftrightarrow\left\{{}\begin{matrix}x+y=-\sqrt{2}\\x=y\end{matrix}\right.\)\(\Leftrightarrow x=y=-\dfrac{\sqrt{2}}{2}\)

c) \(S=\dfrac{1}{ab}+\dfrac{1}{a^2+b^2}=\dfrac{1}{a^2+b^2}+\dfrac{1}{2ab}+\dfrac{1}{2ab}\)

Với x,y>0, ta có: \(\dfrac{1}{x}+\dfrac{1}{y}\ge\dfrac{4}{x+y}\) (1)

Thật vậy (1) \(\Leftrightarrow\dfrac{y+x}{xy}\ge\dfrac{4}{x+y}\Leftrightarrow\left(x+y\right)^2\ge4xy\)\(\Leftrightarrow\left(x-y\right)^2\ge0\) (lđ)

Áp dụng (1) vào S ta được:

\(S\ge\dfrac{4}{a^2+b^2+2ab}+\dfrac{1}{2ab}\)

Lại có: \(ab\le\dfrac{\left(a+b\right)^2}{4}\) \(\Leftrightarrow2ab\le\dfrac{\left(a+b\right)^2}{2}\Leftrightarrow2ab\le\dfrac{1}{2}\)\(\Rightarrow\dfrac{1}{2ab}\ge2\)

\(\Rightarrow S\ge\dfrac{4}{\left(a+b\right)^2}+2=6\)

\(\Rightarrow S_{min}=6\Leftrightarrow a=b=\dfrac{1}{2}\)

Ta có 12 ≥ ( a + b ) 3 + 4 a b ≥ 2 a b 3 + 4 a b . Đặt t = a b , t > 0  thì

12 ≥ 8 t 3 + 4 t 2 ⇔ 2 t 3 + t 2 − 3 ≤ 0 ⇔ ( t − 1 ) ( 2 t 2 + 3 t + 3 ) ≤ 0  

Do 2 t 2 + 3 t + 3 > 0 , ∀ t nên t − 1 ≤ 0 ⇔ t ≤ 1 . Vậy 0 < a b ≤ 1  

Chứng minh được 1 1 + a + 1 1 + b ≤ 2 1 + a b , ∀ a , b > 0  thỏa mãn a b ≤ 1  

Thật vậy, BĐT 1 1 + a − 1 1 + a b + 1 1 + b − 1 1 + a b ≤ 0  

a b − a ( 1 + a ) ( 1 + a b ) + a b − b ( 1 + b ) ( 1 + a b ) ≤ 0 ⇔ b − a 1 + a b a 1 + a − b 1 + b ⇔ ( b − a ) 2 ( a b − 1 ) ( 1 + a b ) ( 1 + a ) ( 1 + b ) ≤ 0  

Do 0 < a b ≤ 1  nên BĐT này đúng

Tiếp theo ta sẽ CM 2 1 + a b + 2015 a b ≤ 2016 , ∀ a , b > 0  thỏa mãn  a b ≤ 1

Đặt t = a b , 0 < t ≤ t  ta được 2 1 + t + 2015 t 2 ≤ 2016  

2015 t 3 + 2015 t 2 − 2016 t − 2014 ≤ 0 ⇔ ( t − 1 ) ( 2015 t 2 + 4030 t + 2014 ) ≤ 0  

BĐT này đúng  ∀ t : 0 < t ≤ 1  

Vậy  1 1 + a + 1 1 + b + 2015 a b ≤ 2016.  Đẳng thức xảy ra a = b = 1

+ x+y=2 ta có bảng

+khi x=0, y=2 ta có BPT 0^{4 +} 2⁴ >= 2

+ khi x= 1, y=1 ta có BPT 1⁴ + 1⁴ >=2

⁺ khi x = 2, y=0 ta có BPT 2⁴ + 0⁴ >=2

Nên x⁴ + y⁴ >=2

có phải thuộc số nguyên dâu bạn

Chắc đề đúng là \(\left(m-1\right)x^2+2\left(m-1\right)x-m\le0\)

Để BPT đã cho có tập nghiệm \(S=\left[a;b\right]\) hữu hạn thì:

\(\left\{{}\begin{matrix}m-1>0\\\Delta'=\left(m-1\right)^2+4m\left(m-1\right)>0\end{matrix}\right.\) \(\Rightarrow m>1\)

Khi đó a; b sẽ là nghiệm của pt bậc 2

\(\Rightarrow\left\{{}\begin{matrix}a+b=-2\\ab=\frac{m}{1-m}\end{matrix}\right.\)

\(a^2+b^2+ab=6\)

\(\Leftrightarrow\left(a+b\right)^2-ab-6=0\)

\(\Leftrightarrow\frac{m}{m-1}-2=0\Rightarrow m=2\)

cảm ơn bạn

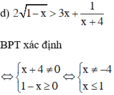
Vậy tập giá trị của x thỏa mãn điều kiện xác định là D = (–∞; 1] \ {–4}.

Điều kiện: x ≥ 0

Ta có:  x  < 2 ⇒  x  < 9 ⇒ x < 9

Điều kiện: x ≥ 0

Ta có:  x  > 2 ⇔  x  >  4  ⇔ x > 4

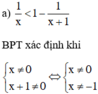
Vậy tập giá trị của x thỏa mãn điều kiện xác định là D = R\{0; –1}