GÓC A SE LÀ 60 ĐỘ

có mà,mình tick bạn rồi, tick lại mình đi

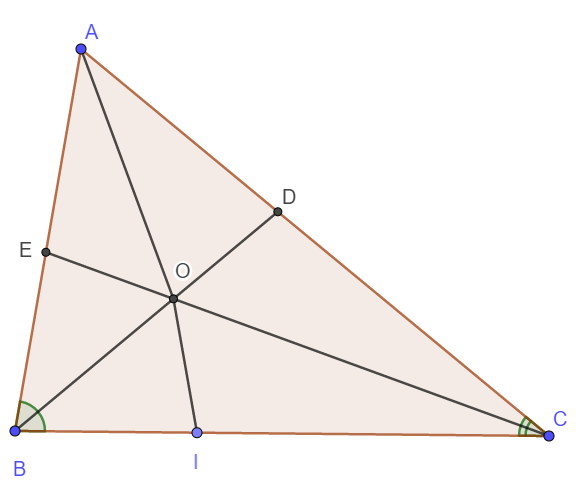
Trên BC lấy điểm I sao cho BI = BE.

Do BC = BE + DC nên IC = DC.

Ta có : \(\Delta EOB=\Delta IOB\left(c-g-c\right)\Rightarrow\widehat{EOB}=\widehat{IOB}\)

\(\Delta DOC=\Delta IOC\left(c-g-c\right)\Rightarrow\widehat{DOC}=\widehat{IOC}\)

Mà \(\widehat{EOB}=\widehat{DOC}\Rightarrow\widehat{EOB}=\widehat{IOB}=\widehat{DOC}=\widehat{IOC}\)

Vậy thì \(\widehat{IOB}=\widehat{DOC}=\widehat{IOC}=\frac{180^o}{3}=60^o\)

\(\Rightarrow\widehat{BOC}=60^o+60^o=120^o\)

\(\Rightarrow\frac{\widehat{B}}{2}+\frac{\widehat{C}}{2}=180^o-120^o=60^o\)

\(\Rightarrow\widehat{B}+\widehat{C}=120^o\Rightarrow\widehat{A}=60^o\)

Câu hỏi của Nguyễn Duy Thịnh - Toán lớp 7 - Học toán với OnlineMath

Em tham khảo tại đây nhé.

Câu hỏi của Nguyễn Duy Thịnh - Toán lớp 7 - Học toán với OnlineMath

Em tham khảo tại đây nhé.

có A = 60 độ (gt)

suy ra c+b=180-60=120

mà c1=1/2 c:b1=1/2 b  ( tích chất tia phân giác )

suy ra c1+b1=120:2=60

suy ra BOC = 180-60=120

B)

xét Tam giác BOE và BOF  bằng nhau theo ( cạnh góc cạnh)

suy ra OB là tia phân giác ủa EOF

C: có Phân giác Ce và BD cắt Nhau tại O 

mà AF cắt CE và BD tại O  suy ra AF LÀ  phân giác của góc BAC

từ đó suy ra  OD=OE=OF ( tích chất  của tia phân giác )

, hình thì m tự vẽ bố éo rảnh ngồi vẽ :))

a) Ta có \(\widehat{B_1}=\widehat{B_2};\widehat{C_1}=\widehat{C_2}\Rightarrow\widehat{B_1}+\widehat{C_1}=\frac{\widehat{B}+\widehat{C}}{2}=\frac{180^o-\widehat{A}}{2}=\frac{180^o-60^o}{2}=60^o\)

Vậy thì \(\widehat{BOC}=180^o-60^o=120^o\)

b) Xét tam giác BEO và BFO có:

BE = BF (gt)

BO chung

\(\widehat{B_1}=\widehat{B_2}\)

\(\Rightarrow\Delta BEO=\Delta BFO\left(c-g-c\right)\)

\(\Rightarrow\widehat{BOE}=\widehat{BOF}\)   (Hai góc tương ứng)

Vậy OB là tia phân giác góc EOF.

c) Gọi K, H là chân đường cao hạ từ O xuống AB và AC

Do O là giao điểm của 3 đường phân giác nên OH = OK 

Ta có \(\widehat{EAD}+\widehat{EOD}=60^o+\widehat{BOC}=60^o+120^o=180^o\)  

\(\Rightarrow\widehat{AEO}+\widehat{ODK}=180^o\Rightarrow\widehat{OEH}=\widehat{ODK}\Rightarrow\widehat{HOE}=\widehat{KOD}\)

Vậy thì \(\Delta OEH=\Delta ODK\)   (Cạnh góc vuông - góc nhọn kề)

\(\Rightarrow OE=OD\)

a: Xét tứ giác BEDF có 

DF//BE

ED//BF

Do đó: BEDF là hình bình hành

mà BD là đường phân giác

nên BEDF là hình thoi

Suy ra: DB là tia phân giác của góc EDF

b: Ta có: ED//BC

nên \(\widehat{AED}=\widehat{ABC};\widehat{ADE}=\widehat{ACB}\)