Câu 3: Cho hình chóp S.ABCD, trong đó ABCD là một hình thang với đáy lớn AD. Gọi H và K lần lượt là trung điểm của AB và DC. Gọi G là trọng tâm của tam giác SAD. Giao tuyến (d) của hai mặt phẳng (SAD) và (GHK). Biết (d) cắt SA tại M và cất SD tại N. Tứ giác MNKH là hình bình hành thì AD =k.BC. Khi đó k =?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan

CM
8 tháng 3 2018
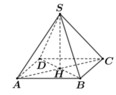
Do SA = SB = SC = SD = a 6 nên hình chiếu vuông góc của S trên mặt phẳng (ABCD) trùng với tâm đường tròn ngoại tiếp đáy. Do đó tứ giác ABCD là hình chữ nhật.
![]()
![]()
![]()
Tam giác vuông SHA có ![]()
Khi đó
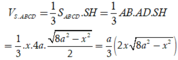
![]()
Chọn A.

NV
Nguyễn Việt Lâm
Giáo viên
27 tháng 7 2021
Trong mp (ABCD), nối MN kéo dài lần lượt cắt AD tại F và DC tại G
Trong mp (SAD), nối FE cắt SA tại P
Trong mp (SCD), nối EG cắt SC tại Q
\(\Rightarrow\) Ngũ giác MNQEP là thiết diện của (MNE) và chóp
Trong mp(SAD) qua G dựng đường thẳng d//AD
HA=HB; KC=KD => HK là đường trung bình của hình thang ABCD
=> HK//AD và \(HK=\dfrac{AB+CD}{2}\)
Ta có d//AD
=> d//HK (cùng // với AD)
\(\Rightarrow d\in\left(GHK\right)\) mà \(d\in\left(SAD\right)\) => d là giao tuyến của (SAD) với (GHK)
Xét tg SAE có MN//AD \(\Rightarrow\dfrac{SM}{SA}=\dfrac{MG}{AE}=\dfrac{SG}{SE}=\dfrac{2}{3}\)
Xét tg SAD có MN//AD \(\Rightarrow\dfrac{MN}{AD}=\dfrac{SM}{SA}=\dfrac{2}{3}\Rightarrow MN=\dfrac{2}{3}AD\)
Do MNHK là hbh => MN=HK
\(\Rightarrow\dfrac{2}{3}AD=\dfrac{AD+BC}{2}\Leftrightarrow4AD=3AD+3BC\)
\(\Leftrightarrow AD=3BC=k.BC\Rightarrow k=3\)