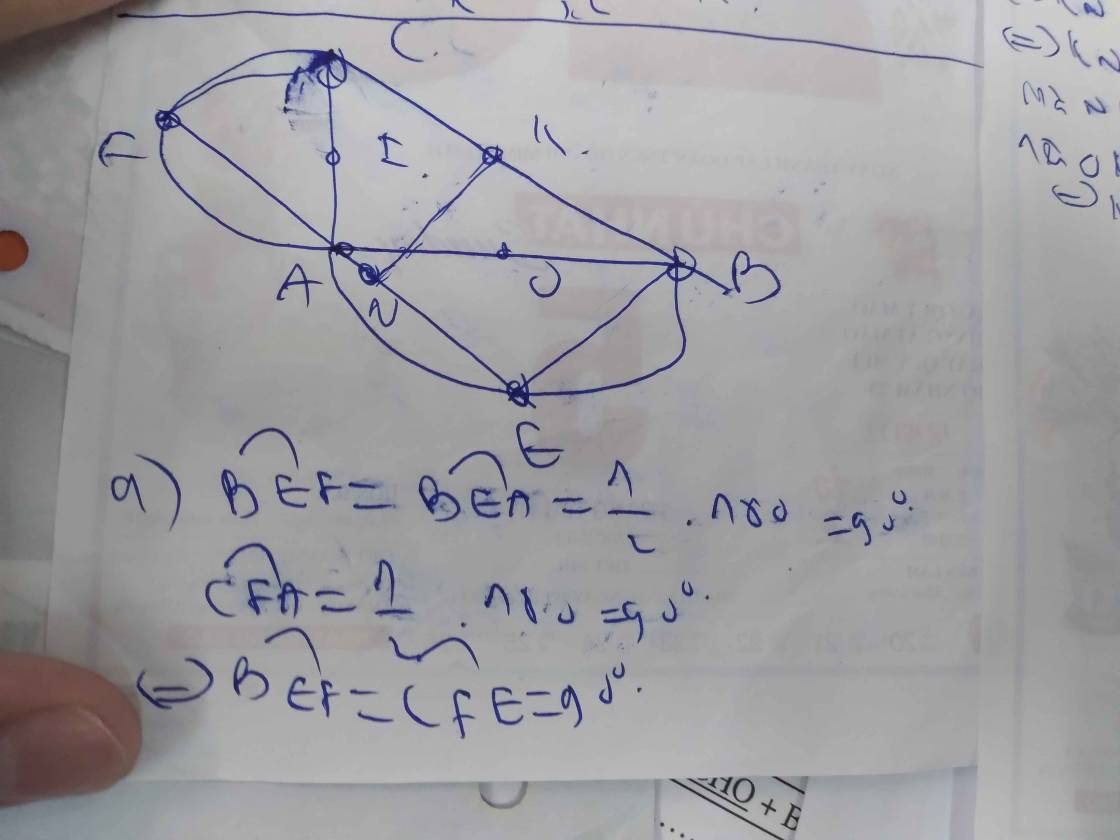
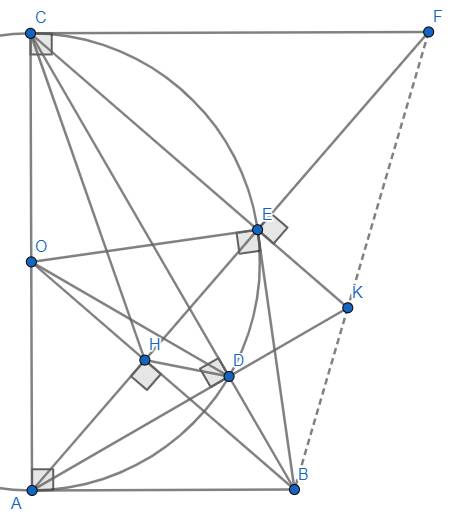
Ở bên ngoài tam giác ABC, vẽ hai nửa đường tròn có đường kính AB và AC. Một đường thẳng d quay quanh A cắt hai nửa đường tròn lần lượt tại D, E (khác A).
a) CMR đường trung trực của đoạn thẳng DE luôn đi qua một điểm cố định.
b) Tìm quỹ tích trung điểm M của đoạn thẳng DE.
c) Xác định vị trí của đường thẳng d để DB + CE đặt giá trị lớn nhất.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a:
ΔABC vuông tại A có AB=AC
nên ΔABC vuông cân tại A
=>góc ABC=góc ACB=45 độ
góc BDA=1/2*sđ cung BA=90 độ
góc EAC=1/2*sđ cung CA=90 độ
BD vuông góc DA
CE vuông góc AE
mà D,A,E thẳng hàng
nên BD//CE
Xét tứ giác BDEC có
góc BDE+góc DEC+góc DBC+góc ECB=360 độ
=>góc DBC+góc ECB=180 độ
=>góc ECA+góc ACB+góc ABD+góc ABC=180 độ
=>góc ECA+góc ABD=90 độ
góc EAC+góc ECA=90 độ
mà góc DBA+góc ECA=90 độ
nên góc EAC=góc DBA
Xét ΔACE vuông tại E và ΔBAD vuông tại D có
AC=AB
góc EAC=góc DBA
=>ΔACE=ΔBAD
=>AD=CE
b: AD^2+AE^2
=CE^2+AE^2
=AC^2=16

a) a1. Chứng minh \(BAOE\) là tứ giác nội tiếp.
Tứ giác \(BAOE:\left\{{}\begin{matrix}\hat{OEB}=90^o\left(\text{tiếp tuyến}\right)\\\hat{OAB}=90^o\left(gt\right)\end{matrix}\right.\)
\(\Rightarrow\hat{OEB}+\hat{OAB}=90^o+90^o=180^o\Rightarrow BAOE\) là tứ giác nội tiếp (đpcm).
a2. Chứng minh : \(BH.BO=BD.BC\).
Ta có : \(\hat{ADC}=90^o\) (góc nội tiếp chắn nửa đường tròn)
\(\Rightarrow AD\) là đường cao của \(\Delta ABC\) vuông tại \(A\Rightarrow BD.BC=AB^2\left(1\right).\)
Mặt khác : \(\left\{{}\begin{matrix}OA=OE=R\left(gt\right)\\AB=BE\left(\text{tính chất hai tiếp tuyến cắt nhau}\right)\end{matrix}\right.\)
\(\Rightarrow OB\) là đường trung trực của \(AE\Rightarrow\hat{AHB}=90^o\)
\(\Rightarrow AH\) là đường cao của \(\Delta ABC\) vuông tại \(A\Rightarrow BH.BO=AB^2\left(2\right).\)
Từ \(\left(1\right),\left(2\right)\Rightarrow BH.BO=BD.BC\) (đpcm).
b) b1. Chứng minh \(DHOC\) là tứ giác nội tiếp.
Tứ giác \(AHDB:\hat{AHB}=\hat{ADB}=90^o\left(cmt\right)\). Mà hai góc này có đỉnh kề nhau trong tứ giác và cùng nhìn cạnh \(AB\) nên đây là tứ giác nội tiếp \(\Rightarrow\hat{ABH}=\hat{ADH}.\)
Mà : \(\left\{{}\begin{matrix}\hat{ADH}+\hat{HDC}=90^o\left(=\hat{ADC}\left(cmt\right)\right)\\\hat{ABH}+\hat{HAB}=90^o\left(\text{hai góc phụ nhau}\right)\end{matrix}\right.\Rightarrow\hat{HDC}=\hat{HAB}\left(3\right).\)
Mặt khác : \(\hat{AOB}=\hat{HAB}\left(\text{cùng phụ }\hat{ABH}\right)\left(4\right).\)
Từ \(\left(3\right),\left(4\right)\Rightarrow\hat{AOB}=\hat{HDC}\Rightarrow DHOC\) là tứ giác nội tiếp (dấu hiệu nhận biết) (đpcm).
b2. Chứng minh : \(\hat{BHD}=\hat{OHC}\).
Do \(DHOC\) là tứ giác nội tiếp (cmt) \(\Rightarrow\hat{OCD}=\hat{BHD}\left(5\right)\) (cùng bù với \(\hat{OHD}\)) và \(\hat{OHC}=\hat{ODC}\left(6\right)\) (hai góc có đỉnh kề nhau cùng nhìn cạnh \(OC\)).
Mặt khác : \(OA=OD=R\Rightarrow\Delta OAD\) cân tại \(O\Rightarrow\hat{ODA}=\hat{OAD}.\)
Và : \(\left\{{}\begin{matrix}\hat{OAD}+\hat{OCD}=90^o\left(\text{hai góc phụ nhau}\right)\\\hat{ODA}+\hat{ODC}=90^o\left(=\hat{ADC}\right)\end{matrix}\right.\Rightarrow\hat{OCD}=\hat{ODC}\left(7\right).\)
Từ \(\left(5\right),\left(6\right),\left(7\right)\Rightarrow\hat{BHD}=\hat{OHC}\) (đpcm).
c) Chưa nghĩ ra ạ:)

Bạn muốn nhận giày và balo miễn phí cho năm học mới? --->Tham gia ngay Minigame NHANH NHƯ CHỚP số thứ 7 ngày 16/02/2019 tại đây: https://alfazi.edu.vn/question/5c6818c4641b064a18a2575b Cơ hội rất hiếm! Hôm qua bạn Thiên An vừa nhận được 1 balo trị giá 350k đấy! Xem chi tiết :https://alfazi.edu.vn/question/5c6818c4641b064a18a2575b
ALFAZI THƯƠNG HIỆU HỌC TẬP SỐ 1 VN!
a) Ta thấy: Các góc ^AMB, ^ANC nội tiếp chắn nửa đường tròn => ^AMB = ^ANC = 900
=> BM và CN cùng vuông góc MN => BM // CN
Xét tứ giác BMNC: BM // CN, ^BMN = ^CNM = 900 => Tứ giác BMNC là hình thang vuông.
b) Gọi AK là trung tuyến từ đỉnh A của \(\Delta\)ABC. Dễ thấy IK là đường trung bình hình thang BMNC
=> IK // BM // CN. Mà BM,CN vuông góc MN nên IK vuông góc MN tại I => ^AIK = 900
=> I nằm trên đường tròn đường kính AK . Do AK cố định nên (AK) cố định
=> I chạy trên đường tròn (AK). Kết luận: ...