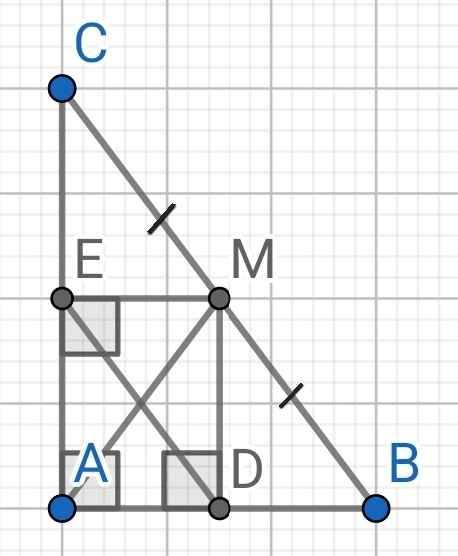
Cho tam giác ABC vuông tại A, trên cạnh BC lấy M. Gọi D,E lần lượt là hình chiếu của M trên cạnh AB, AC. Tứ giác ADME là gì? Vì sao?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) ADME là hình chữ nhật vì có 3 góc vuông: \(\widehat{A}\)= \(\widehat{D}\)= \(\widehat{E}\)= 900
b) Để ADME là hình vuông thì AM là phân giác \(\widehat{A}\)
Vậy M là giao đường phân giác góc A với BC thì ADME là hình vuông

a: Xét tứ giác ADME có
góc ADM=góc AEM=góc DAE=90 độ
=>ADME là hình chữ nhật
b: ADME là hình chữ nhật
=>AM cắt DE tại trung điểm của mỗi đường
mà I là trung điểm của DE
nên I là trung điểm của AM
=>A,I,M thẳng hàng
c: Xét ΔBMP có
BD vừa là đường cao, vừa là đường trung tuyến
Do đó: ΔBMP cân tại B
=>BA là phân giác của góc MBP
Xét ΔAMP có
AD là đường cao, là đường trung tuyến
Do đó: ΔAMP cân tại A
=>AB là phân giác của góc MAP(1)
Xét ΔAMQ có
AC vừa là đường cao, vừa là đường trung tuyến
Do đó; ΔAMQ cân tại A
=>AC là phân giác của góc MAQ(2)
Từ (1), (2) suy ra góc PAQ=2*góc BAC=180 độ
=>P,A,Q thẳng hàng
Xét ΔAMB và ΔAPB có
AM=AP
AB chung
BM=BP
Do đó: ΔAMB=ΔAPB
=>góc AMB=góc APB
Xét ΔAMC và ΔAQC có
AM=AQ
góc MAC=góc QAC
AC chung
Do đó: ΔAMC=ΔAQC
=>góc AMC=góc AQC
=>góc AQC+góc AMB=180 độ
mà góc AMB=góc APB
nên góc AQC+góc APB=180 độ
=>BP//QC
=>BPQC là hình thang
d: AM=AP
AM=AQ
Do đó: AP=AQ
mà P,A,Q thẳng hàng
nên A là trung điểm của PQ

a)\(\Delta ABC\) vuông tại A nên \(\widehat{BAC}=90^o\Rightarrow\widehat{DAE}=90^o\)
Có D là hình chiếu của M trên AB \(\Rightarrow MD\perp AB\Rightarrow\widehat{MDA}=90^o\)
Có E là hình chiếu của M trên AC \(\Rightarrow ME\perp AC\Rightarrow\widehat{AEM}=90^o\)
Xét tứ giác: \(ADEM\) có \(\left\{{}\begin{matrix}\widehat{DAE}=90^o\\\widehat{MDA}=90^o\\\widehat{AEM}=90^o\end{matrix}\right.\)
\(\Rightarrow\)Tứ giác ADEM là hình chữ nhật
Vậy tứ giác ADEM là hình chữ nhật.
b)\(\Delta ABC\) vuông tại A có AM là trung tuyến (M là trung điểm BC)
\(\Rightarrow AM=\dfrac{1}{2}BC\)
Mà \(AM=DE\) (tính chất hcn)
\(\Rightarrow DE=\dfrac{1}{2}BC\left(đpcm\right)\)
Bổ sung đề: Tam giác ABC vuông tại A
 a) Xét tứ giác ADME có:
a) Xét tứ giác ADME có:
∠AEM = ∠EAD = ∠ADM = 90⁰ (gt)
⇒ ADME là hình chữ nhật
b) Do ADME là hình chữ nhật (cmt)
⇒ AM = DE (1)
Lại có:
AM là đường trung tuyến ứng với cạnh huyền BC
⇒ AM = BC/2 (2)
Từ (1) và (2) ⇒ DE = BC/2

a: Xét tứ giác ADME có
\(\widehat{ADM}=\widehat{AEM}=\widehat{DAE}=90^0\)
=>ADME là hình chữ nhật
b: ADME là hình chữ nhật
=>AD//EM và AD=EM(1)
M là trung điểm của EK
=>\(EK=2EM\left(2\right)\)
A là trung điểm của ID
=>\(ID=2DA\left(3\right)\)
Từ (1),(2),(3) suy ra EK=ID
EM//AD
K\(\in\)EM
I\(\in\)AD
Do đó: EK//ID
Xét tứ giác EKDI có
EK//DI
EK=DI
Do đó: EKDI là hình bình hành

a: Xét tứ giác AIMJ có
\(\widehat{AIM}=\widehat{AJM}=\widehat{JAI}=90^0\)
=>AIMJ là hình chữ nhật
b: AIMJ là hình chữ nhật
=>MI//AJ và MI=AJ
MI=AJ
MN=MI
Do đó: MN=AJ
MI//AJ
N\(\in\)MI
Do đó: MN//JA
Xét tứ giác AMNJ có
AJ//MN
AJ=MN
Do đó: AMNJ là hình bình hành

a: Xét tứ giác ADME có
\(\widehat{ADM}=\widehat{AEM}=\widehat{DAE}=90^0\)
Do đó: ADME là hình chữ nhật
\(\widehat{MDA}=1v\)( Vì MD vuông góc AB )
\(\widehat{MEA}=1v\)( vì ME vuông góc AC )
\(\widehat{BAC}=1v\)( gt )
\(\Rightarrow\)ADME - hình chữ nhật ( đpcm )
Cảm ơn bạn Hiếu
Mình đã hiểu cách làm rồi