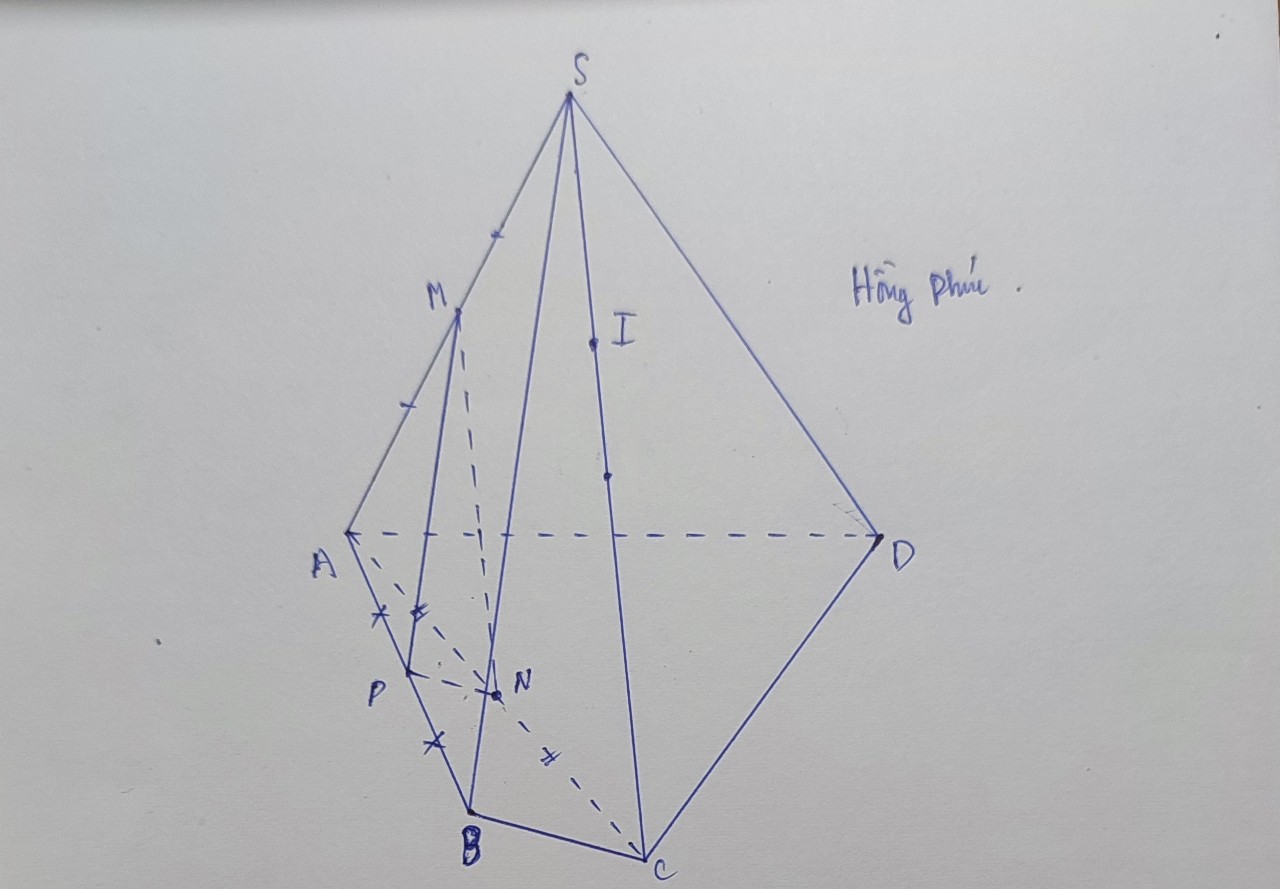
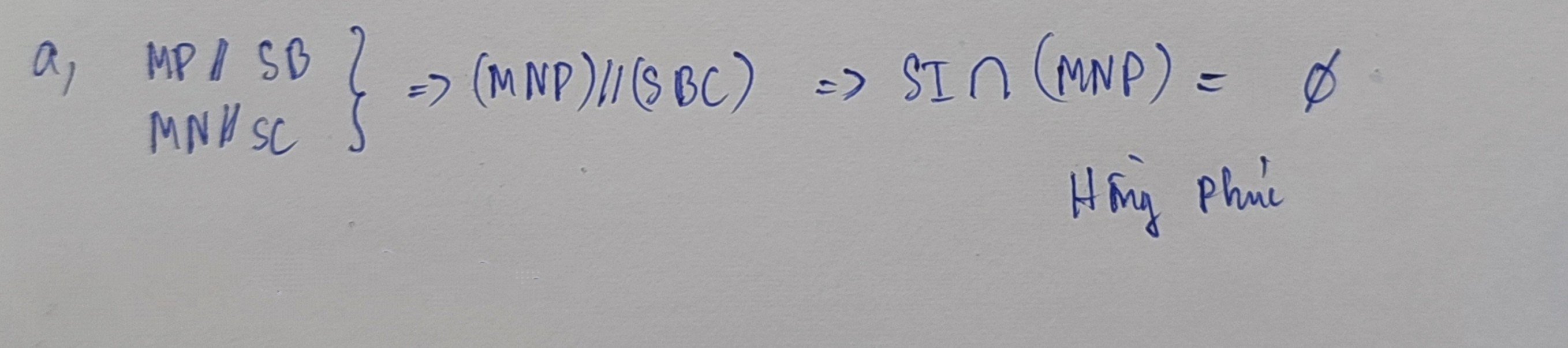
a/ Qua S dựng đường thẳng d//AD

d//AD; \(S\in\left(SAD\right)\Rightarrow d\in\left(SAD\right)\)

d//AD;AD//BC => d//BC mà \(S\in\left(SBC\right)\Rightarrow d\in\left(SBC\right)\)

=> d chính là giao tuyến của (SAD) và (SBC)

b/

Trong (SAC) gọi I là giao của AM với SO

\(I\in SO;SO\in\left(SBD\right)\Rightarrow I\in\left(SBD\right)\)

=> I là giao của AM với (SBD)

Ta có BC//AD \(\Rightarrow\dfrac{OC}{OA}=\dfrac{BC}{AD}=\dfrac{1}{2}\)

2 tg SAM và tg CAM có chung đường cao từ A->SC và MS=MC nên \(S_{SAM}=S_{CAM}=S\)

2 tg AMO và tg CMO có chung đường cao từ M->AC nên

\(\dfrac{S_{AMO}}{S_{CMO}}=\dfrac{OA}{OC}=2\Rightarrow\dfrac{S_{AMO}}{2}=S_{CMO}=\dfrac{S_{AMO}+S_{CMO}}{2+1}=\dfrac{S_{CAM}}{3}\)

\(\Rightarrow\dfrac{S_{AMO}}{S_{CAM}}=\dfrac{S_{AMO}}{S_{SAM}}=\dfrac{2}{3}\)

2 tg AMO và tg SAM có chung AM nên

\(\dfrac{S_{AMO}}{S_{SAM}}=\) đường cao từ O->AM/đường cao từ S->AM \(=\dfrac{2}{3}\)

2 tg OMI và tg SMI có chung IM nên

\(\dfrac{S_{OMI}}{S_{SMI}}=\)đường cao từ O->AM/đường cao từ S->AM\(=\dfrac{2}{3}\)

2tg OMI và tg SMI có chung đường cao từ M->SO nên

\(\dfrac{S_{OMI}}{S_{SMI}}=\dfrac{OI}{SI}=\dfrac{2}{3}\)

\(\Rightarrow\dfrac{OI}{2}=\dfrac{SI}{3}=\dfrac{OI+SI}{2+3}=\dfrac{SO}{5}\Rightarrow\dfrac{SI}{SO}=\dfrac{3}{5}\)

 c/

Gọi P là trung điểm của SA, Xét tg SAD có

PA=PS; ND=NS (gt) => PN là đường trung bình của tg SAD

=> PN//AD và \(PN=\dfrac{1}{2}AD\) 

Ta có

PN//AD; AD//BC => PN//BC

\(AD=2BC\Rightarrow BC=\dfrac{1}{2}AD\)

=> PN//BC và \(PN=BC=\dfrac{1}{2}AD\)

=> BCNP là hbh (Tứ giác có 1 cặp cạnh đối // và bằng nhau là hbh)

=> CN//BP (cạnh đối hbh) mà \(BP\in\left(SAB\right)\) => CN//(SAB)

a.

Qua S kẻ đường thẳng d song song AD và BC

Do \(\left\{{}\begin{matrix}S\in\left(SAD\right)\\S\in d\\d||AD\end{matrix}\right.\) \(\Rightarrow d\in\left(SAD\right)\)

\(\left\{{}\begin{matrix}S\in\left(SBC\right)\\S\in d\\d||BC\end{matrix}\right.\) \(\Rightarrow d\in\left(SBC\right)\)

\(\Rightarrow d=\left(SAD\right)\cap\left(SBC\right)\)

b.

Trong mp (SAC), nối AM cắt SO tại I

\(\left\{{}\begin{matrix}O\in BD\in\left(SBD\right)\\S\in\left(SBD\right)\end{matrix}\right.\) \(\Rightarrow SO\in\left(SBD\right)\)

\(I\in SO\Rightarrow I\in\left(SBD\right)\)

\(\Rightarrow I=AM\cap\left(SBD\right)\)

Do AD song song BC, áp dụng định lý Thales:

\(\dfrac{OA}{OC}=\dfrac{AD}{BC}=2\) \(\Rightarrow OA=2OC=2\left(AC-OA\right)\Rightarrow\dfrac{OA}{AC}=\dfrac{2}{3}\)

Áp dụng định lý Menelaus:

\(\dfrac{OA}{AC}.\dfrac{CM}{MS}.\dfrac{SI}{IO}=1\Leftrightarrow\dfrac{2}{3}.1.\dfrac{SI}{IO}=1\)

\(\Rightarrow2SI=3IO=3\left(SO-SI\right)\)

\(\Rightarrow5SI=3SO\Rightarrow\dfrac{SO}{SI}=\dfrac{3}{5}\)