
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đáp án A
Phương pháp: Đối với tích 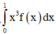 , sử dụng phương pháp tích phân từng phần.
, sử dụng phương pháp tích phân từng phần.
Tìm k để 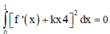
Cách giải:
Ta có 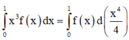
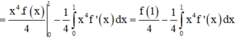
Mà 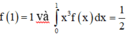
suy ra 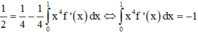
Xét 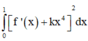
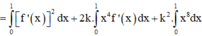
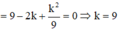
Khi đó 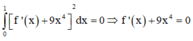
![]()
Mặt khác 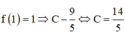
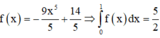

Đáp án B.
Ta có ∫ 0 1 f ' x . c o s π x d x
= ∫ 0 1 c o s π x d f x = f x . c o s π x 0 1 − ∫ 0 1 f x . c o s π x ' d x
= − f 1 + f 0 + π ∫ 0 1 f x . sin π x d x = π 2 ⇒ ∫ 0 1 f x . sin π x d x = 1 2 .
Xét ∫ 0 1 f x + k . sin π x 2 d x = 0
⇔ ∫ 0 1 f 2 x d x + 2 k . ∫ 0 1 f x . sin π x d x + k 2 . ∫ 0 1 sin 2 π x d x = 0
⇔ 1 2 k 2 + 2 k . 1 2 + 1 2 = 0 ⇔ k + 1 2 = 0 ⇔ k = − 1.
Suy ra ∫ 0 1 f x − sin π x 2 d x = 0.
Vậy f x = sin π x ⇒ ∫ 0 1 f x d x = ∫ 0 1 sin π x d x = 2 π .

Đáp án C
Ta có I = ∫ 1 2 2 f x x d x = I = ∫ 1 2 2 1 x 3 x − 2 f 1 x d x = 3 ∫ 1 2 2 d x − 2 ∫ 1 2 2 1 x f 1 x d x
Đặt t = 1 x ⇔ d t = − d x x 2 ⇔ d x = − d t t 2 và x = 1 2 ⇒ t = 2 x = 2 ⇒ t = 1 2 .
Suy ra ∫ 1 2 2 1 x f 1 x d x = ∫ 1 2 2 f t t d t
Vậy I = 3 ∫ 1 2 2 d x − 2 ∫ 1 2 2 f t t d t = 9 2 − 2 ∫ 1 2 2 f t t d t ⇒ 3 I = 9 2 ⇔ I = 3 2

Đáp án A
Đặt I = 1 2 x . f x d x
1 3 f x + 1 d x = 2 1 2 u f u d u ⇒ 1 2 x f x d x = 8 2 = 4.
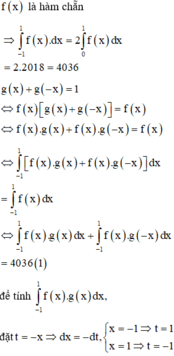
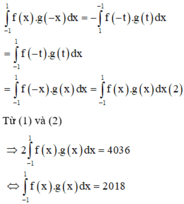
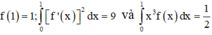 .
. 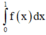
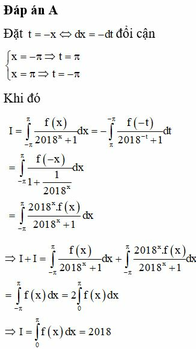
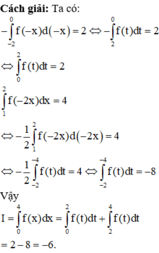
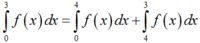
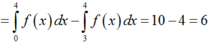
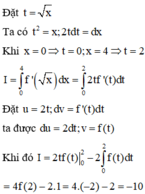
Ta có \(\sqrt{2+2\cos2x}=\sqrt{2+2\left(2\cos^2x-1\right)}=\sqrt{4\cos^2x}=2\left|\cos x\right|\)
\(\Leftrightarrow f\left(x\right)+f\left(-x\right)=2\left|\cos x\right|,\forall x\inℝ\) (1)
Đặt \(g\left(x\right)=f\left(x\right)-\left|\cos x\right|\)
Khi đó (1) \(\Leftrightarrow\left[f\left(x\right)-\left|\cos x\right|\right]+\left[f\left(-x\right)-\left|\cos x\right|\right]=0\)
\(\Leftrightarrow g\left(x\right)+\left[f\left(-x\right)-\left|\cos\left(-x\right)\right|\right]=0\) (do \(\cos x\) là hàm chẵn)
\(\Leftrightarrow g\left(x\right)+g\left(-x\right)=0\)
\(\Leftrightarrow g\left(x\right)=-g\left(-x\right)\)
\(\Leftrightarrow g\left(x\right)\) là hàm lẻ
Khi đó \(f\left(x\right)=g\left(x\right)+\left|\cos x\right|\) với \(g\left(x\right)\) là hàm lẻ. Thử lại, ta thấy:
(1) \(\Leftrightarrow f\left(x\right)+f\left(-x\right)=g\left(x\right)+\left|\cos x\right|+g\left(-x\right)+\left|\cos\left(-x\right)\right|\)
\(\Leftrightarrow f\left(x\right)+f\left(-x\right)=2\left|\cos x\right|\), thỏa mãn
Vậy \(f\left(x\right)=g\left(x\right)+\left|\cos x\right|\) với \(g\left(x\right)\) là hàm lẻ bất kì có tập xác định là \(ℝ\)
\(\Rightarrow I=\int\limits^{\dfrac{3\pi}{2}}_{-\dfrac{3\pi}{2}}f\left(x\right)dx\)
\(I=\int\limits^{\dfrac{3\pi}{2}}_{-\dfrac{3\pi}{2}}\left[g\left(x\right)+\left|\cos x\right|\right]dx\)
\(I=\int\limits^{\dfrac{3\pi}{2}}_{-\dfrac{3\pi}{2}}g\left(x\right)dx+\int\limits^{\dfrac{3\pi}{2}}_{-\dfrac{3\pi}{2}}\left|\cos x\right|dx\)
\(I=\int\limits^{\dfrac{3\pi}{2}}_{-\dfrac{3\pi}{2}}\left|\cos x\right|dx\) (do \(g\left(x\right)\) là hàm lẻ)
\(I=\int\limits^{-\dfrac{\pi}{2}}_{-\dfrac{3\pi}{2}}\left(-\cos x\right)dx+\int\limits^{\dfrac{\pi}{2}}_{-\dfrac{\pi}{2}}\cos xdx+\int\limits^{\dfrac{3\pi}{2}}_{\dfrac{\pi}{2}}\left(-\cos x\right)dx\)
\(I=-\sin x|^{-\dfrac{\pi}{2}}_{-\dfrac{3\pi}{2}}+\sin x|^{\dfrac{\pi}{2}}_{-\dfrac{\pi}{2}}-\sin x|^{\dfrac{3\pi}{2}}_{\dfrac{\pi}{2}}\)
\(I=6\)