\(\frac{a}{b}\)= \(\frac{3}{d}\)

\(\Rightarrow\)\(-\frac{a}{b}\)= \(-\frac{c}{d}\)

\(\Rightarrow\)1 + \(-\frac{a}{b}\)= 1 + \(-\frac{c}{d}\)

\(\Rightarrow\)\(\frac{b-a}{b}\)= \(\frac{d-c}{d}\)( dpcm)

a/b = c/d => 1 - a/b = 1 - c/d

              => b/b - a/b = d/d - c/d

              => (b - a)/b = (d - c)/d

\(\frac{a}{b}=\frac{c}{d}\)

\(\Rightarrow\frac{-a}{b}=\frac{-c}{d}\)

\(\Rightarrow1+\frac{-a}{b}=1+\frac{-c}{d}\)

\(\Rightarrow\frac{b-a}{b}=\frac{d-c}{d}\left(dpcm\right)\)

Đề sai/ thiếu. Cho $a=0; b=1; c=2$ thì $a^3a^3+b^3b^3+c^3c^3=65$ còn $3abc=0$

a) Để \(\overrightarrow u  = \overrightarrow v  \Leftrightarrow \left\{ \begin{array}{l}2a - 1 = 3\\ - 3 = 4b + 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 2\\b =  - 1\end{array} \right.\)

Vậy \(\left\{ \begin{array}{l}a = 2\\b =  - 1\end{array} \right.\) thì \(\overrightarrow u  = \overrightarrow v \)

b) \(\overrightarrow x  = \overrightarrow y  \Leftrightarrow \left\{ \begin{array}{l}a + b = 2a - 3\\ - 2a + 3b = 4b\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 1\\b =  - 2\end{array} \right.\)

Vậy \(\left\{ \begin{array}{l}a = 1\\b =  - 2\end{array} \right.\) thì \(\overrightarrow x  = \overrightarrow y \)

a.1/3=5/15=9/27=135/405

b.63/35=54/30=45/25

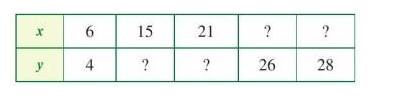
a) Hệ số tỉ lệ của y đối với x là: k₁ =\(\frac{6}{4} = \frac{3}{2}\). Công thức tính y theo x là: y = k₁ . x = \(\frac{3}{2}\).x

b) Hệ số tỉ lệ của x đối với y là: k₂ =\(\frac{4}{6} = \frac{2}{3}\). Công thức tính x theo y là: x = k₂ . y = \(\frac{2}{3}\).y

c)

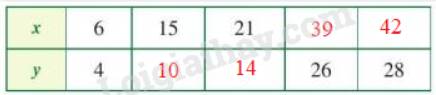
Chú ý:

Nếu đại lượng y tỉ lệ thuận với đại lượng x theo hệ số tỉ lệ k thì đại lượng x tỉ lệ thuận với đại lượng y theo hệ số tỉ lệ \(\frac{1}{k}\).

Chọn A.

Số có 4 chữ số khác nhau các được lập từ các số 3,5,7,9 là một chỉnh hợp chập 4 của 4

Như vậy ta có \(^4_4A\) =24số.

Số có 4 chữ số có dạng: \(\overline{abcd}\)

a có 4 cách chọn.

b có 3 cách chọn.

c có 2 cách chọn.

d có 1 cách chọn.

\(\Rightarrow\) Lập được \(4.3.2.1=24\) số tự nhiên thỏa mãn.

a: \(\left\{{}\begin{matrix}n+2⋮d\\n+3⋮d\end{matrix}\right.\Leftrightarrow1⋮d\Leftrightarrow d=1\)

Vậy: với mọi số nguyên n thì n+2 và n+3 là hai số nguyên tố cùng nhau