Cho x - y = -3 hãy tính giá trị của biểu thức P=x^3 + 3x^2 + y^2 - x²y - xy + x - 4y + 2023 (đề thi học sinh giỏi 7 huyện Nam đàn , tỉnh nghệ An 2022 - 2023 )
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

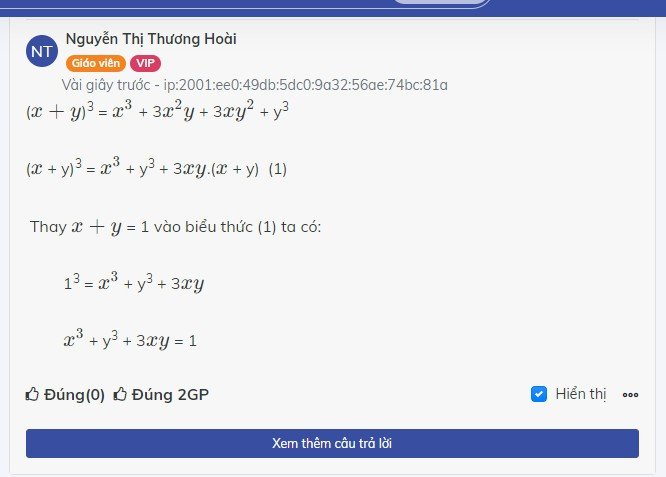
a) cho x+y=1. Tính giá trị biểu thức x^3+ y^3+ 3xy
b) cho x-y=1. Tính giá trị biểu thức x^3- y^3- 3xy

x^3+ y^3+ 3xy
=(x+y)(x^2 -xy + y^2 ) + 3xy
=x^2 -xy + y^2 + 3xy
=x^2 + 2xy + y^2
=(x+y)^2 =1
=> x^3+ y^3+ 3xy=1

a, \(M=2x^3+xy^2-3xy+1\)
b, Thay x = -1 ; y = 2 ta được
M = -2 - 2 + 6 + 1 = 3

\(A = {x^2}y + 2xy - 3{y^2} + 4\)
Thay các x = -2 và y = 3 vào công thức ta có :
\(\begin{array}{l}A = {( - 2)^2}.3 + 2( - 2).3 - {3.3^2} + 4\\ = 4.3 - 12 - 27 + 4\\ = - 23\end{array}\)

a) Thay x = -1 và y = 3 vào A, ta được :
A = 2.(-1)[(-1) + 3] - (-1) + 7 - 3
A = -2.2 + 1 + 4
A = -4 + 5
A = 1
b) |y| = 3 => \(\orbr{\begin{cases}y=3\\y=-3\end{cases}}\)
*Thay x =-1 và y = 3 vào biểu thức :
Phần này bạn sẽ làm ý như câu a vậy :33
*Thay x = -1 và y =-3 vào A, ta được :
A = 2.(-1).[(-1) + (-3)] - (-1) + 7 - (-3)
A = -2.(-4) + 1 + 7 + 3
A = 8 + 11
A = 19

13 = (\(x+y\))3 = \(x^3\) + 3\(x^2\)y + 3\(xy^2\) + y3 = \(x^3\)+y3+3\(xy\)(\(x+y\))
1 = \(x^3\)+y3+3\(xy\)
13 = (\(x-y\))3 = \(x^3\) - 3\(x^2\)y + 3\(xy\) - y3 = \(x^3\) - y3 - 3\(xy\)(\(x-y\))
1 = \(x^3\) - y3 - 3\(xy\)

b; 13 = (\(x-y\))3 = \(x^3\) - 3\(x^2\).y + 3\(xy^2\) - y3 = \(x^3\) - y3 - 3\(xy\)(\(x-y\))
1 = \(x^3\) - y3 - 3\(xy\)
\(x-y=-3\Leftrightarrow x+3=y\)
\(P=x^2\left(x+3\right)+y^2-x^2y-xy+x-4y+2003=\)
\(=x^2y+y^2-x^2y-xy+x-4y+2023=\)
\(=y^2-xy-3y+x-y+2023=\)
\(=y^2-y\left(x+3\right)+x-y+2003=\)
\(=y^2-y^2+\left(x-y\right)+2023=-3+2023=2000\)