a: Xét tứ giác AHMK có

\(\widehat{AHM}=\widehat{AKM}=\widehat{HAK}=90^0\)

=>AHMK là hình chữ nhật

=>AM=HK

b: Xét ΔABC có

M là trung điểm của BC

MK//AB

Do đó: K là trung điểm của AC

Xét ΔABC có

M là trung điểm của BC

MH//AC

Do đó: H là trung điểm của AB

Xét ΔABC có

M,K lần lượt là trung điểm của CB,CA

=>MK là đường trung bình của ΔABC

=>MK//AB và \(MK=\dfrac{AB}{2}\)

Ta có: MK//AB

H\(\in\)AB

Do đó: MK//HB

Ta có: \(MK=\dfrac{AB}{2}\)

\(AH=HB=\dfrac{AB}{2}\)

Do đó: MK=AH=HB

Xét tứ giác BHKM có

BH//KM

BH=KM

Do đó: BHKM là hình bình hành

c: Gọi O là giao điểm của AM và KH

Ta có: AHMK là hình chữ nhật

=>AM cắt KH tại trung điểm của mỗi đường

=>O là trung điểm của AM và KH

=>\(OA=OM=\dfrac{AM}{2};OK=OH=\dfrac{KH}{2}\)

mà AM=KH

nên OA=OM=OK=OH(1)

Xét ΔAKM có

AF,KO là các đường trung tuyến

AF cắt KO tại D

Do đó: D là trọng tâm của ΔAKM

Xét ΔAKM có

D là trọng tâm

KO là đường trung tuyến

Do đó: \(KD=\dfrac{2}{3}KO\left(2\right)\)

Xét ΔHAM có

AE,HO là các đường trung tuyến

AE cắt HO tại I

Do đó: I là trọng tâm của ΔHAM

Xét ΔHAM có

HO là đường trung tuyến

I là trọng tâm

Do đó: \(HI=\dfrac{2}{3}HO\left(3\right)\)

Từ (1),(2),(3) suy ra HI=KD

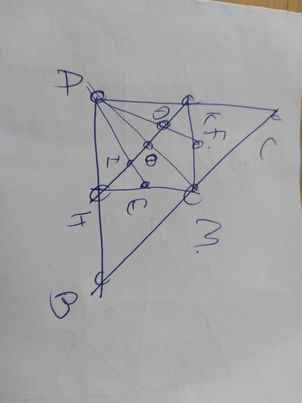
a, tứ giác AKHM có

∠AHM= ∠AKM =∠HAK ( =90 )

⇒ tứ giác AKHM là hình chữ nhật 

b)Ta có tam giác ABC có M trug điểm BC

NH vuông góc vs AB=> MH// AC và MH =1/2 AC

Cmtt K là trung điểm AC

=> HK là đg tb của tam giác ABC=> HK//B M   Ta có HB= MK( Cùng=HA) => tứ giác BHKM là hình bình hành

c)Ta có EF là đường tb tam giác MHK

=> EF//HK 

EF// HK và EF=1/2 HK

GỌI O LÀ GIAO ĐIỂM CỦA HK VÀ AM

EF= HO= KO

Mà HO= HI+IO

=> KO=JO+KJ

Mà IO= JO=> HI= KJ

d) Dễ thấy EF =1/3 AB= 4 căn 3 /3

a: Xét tứ giác AKMH có 

\(\widehat{AKM}=\widehat{AHM}=\widehat{HAK}=90^0\)

Do đó: AKMH là hình chữ nhật

a) .

Xét tam giác ABH và tam giác MBH có :

AB = BH(BE là tia phân giác)

góc ABH = góc HBM(BE là tia phân giác)

BH cạnh chung

đo đó : tam giác ABH = tam giác MBH (c.g c) (1)

b)

 Từ (1) suy ra:

tam giác ABM cân tại B mà BH là phân giác

=>BE là trung trực của đoạn thẳng AM

a/xét tg AMB và tg AMC:

  góc AMB=góc AMC(=90 độ)

 BM=CM(giả thiết)

AM:chung

\(\Rightarrow\)tg AMB=tg AMC(C-G-C)

b/Theo phần a ta có:tg AMB=tg AMC

                             \(\rightarrow\)góc B=góc C(2 góc tương ứng)

c/xét tg BHM và tg CKM:

góc B=góc C(theo phần b)

góc BHM=góc MKC=90 độ

BM=MC(gt)

\(\Rightarrow\)tg BHM= tg CKM(cạnh huyền-góc nhọn)

\(\rightarrow\)MH=MK(2 cạnh tương ứng)

a: Ta có: ΔABC cân tại A

mà AM là đường phân giác

nên M là trung điểm của BC

hay BM=CM

b: Ta có; ΔABC cân tại A

mà AM là đường trung tuyến

nên AM là đường cao

c: Xét ΔAHM vuông tại H và ΔAKM vuông tại K có 

AM chung

\(\widehat{HAM}=\widehat{KAM}\)

Do đó: ΔAHM=ΔAKM

Suy ra: MH=MK

d: Xét ΔBHM vuông tại H và ΔCKM vuông tại K có

MB=MC

MH=MK

Do đó: ΔBHM=ΔCKM

Tham khảo:
 

a: Ta có: ΔABC cân tại A

mà AM là đường phân giác

nên M là trung điểm của BC

hay BM=CM

b: Ta có; ΔABC cân tại A

mà AM là đường trung tuyến

nên AM là đường cao

c: Xét ΔAHM vuông tại H và ΔAKM vuông tại K có 

AM chung

Do đó: ΔAHM=ΔAKM

Suy ra: MH=MK

d: Xét ΔBHM vuông tại H và ΔCKM vuông tại K có

MB=MC

MH=MK

Do đó: ΔBHM=ΔCKM