Bài 2 : Tính chiều cao của hình lăng trụ đứng ABCD . EFGH, biết rằng đáy ABCD là hình thoi có các đường chéo AC = 10cm, Bd= 24cm và diện tích toàn phần bằng 1280 cm^2
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


S đáy=1/2*8*6=3*8=24cm2
348=2*24+S xq
=>Sxq=300cm2
\(AB=\sqrt{\left(\dfrac{8}{2}\right)^2+\left(\dfrac{6}{2}\right)^2}=5\left(cm\right)\)
\(C_{đáy}=4\cdot5=20\left(cm\right)\)
=>h=300/20=15cm

Gọi đường chéo của hình thoi là d và chu vi đáy là p.
Ta có hệ phương trình sau:
d + d = 24cm (vì đường chéo của hình thoi bằng 24cm)
p = 52cm (vì chu vi đáy của hình thoi bằng 52cm)
Từ đó, ta có:
2d = 24cm
d = 12cm
Vậy đường chéo của hình thoi là 12cm.
Để tính chiều cao của hình lăng trụ, ta sử dụng định lý Pytago:
Chiều cao của hình lăng trụ = căn bậc hai của (d^2 - (cạnh đáy/2)^2)
= căn bậc hai của (12^2 - (10/2)^2)
= căn bậc hai của (144 - 25)
= căn bậc hai của 119
≈ 10.92cm
Vậy chiều cao của hình lăng trụ là khoảng 10.92cm.
Để tính thể tích của hình lăng trụ, ta sử dụng công thức:
Thể tích = diện tích đáy x chiều cao
= (diện tích hình thoi x 2) x chiều cao
= (cạnh đáy x cạnh đáy x sin(góc giữa hai đường chéo) x 2) x chiều cao
= (10cm x 10cm x sin(90°) x 2) x 10.92cm
= (100cm^2 x 1 x 2) x 10.92cm
= 2184cm^3
Vậy thể tích của hình lăng trụ là 2184cm^3


Vì ABCD là hình thoi nên A C ⊥ B D tại trung điểm O của AC và BD (ai đường chéo của hình thoi)



Vì ABCD là hình thoi nên A C ⊥ B D tại trung điểm O của AC và BD (ai đường chéo của hình thoi)



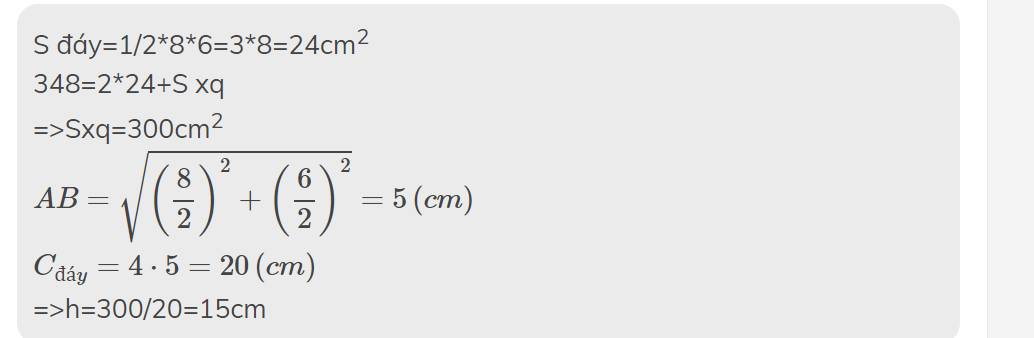


Ta có: AO=\(\dfrac{AC}{2}\)=5 cm
DO=\(\dfrac{BD}{2}\)=12 cm
Áp dụng định lý Pitago vào △AOD
⇒ AO2+DO2=AD2 ⇒ AD=√(AO2+DO2)=13 cm
Gọi h là chiều cao của hình lăng trụ đó
nên Sxq ABCD.EFGH=4.13.h=52h cm2
S2 đáy=2.\(\dfrac{1}{2}\).10.24=240 cm2
Ta có: Stp ABCD.EFGH=Sxq ABCD.EFGH+S2 đáy
⇒ 52h+240=1280 ⇒ h=20 cm
Nên chiều cao của hình lăng trụ đó là 20 cm