Cho hình thoi. ABCD có cạnh bằng 2 và góc B bằng 60. Tìm góc giữa (AB, DA)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đáp án B
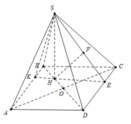
Gọi H là trọng tâm Δ A B C
Dựng H K ⊥ A B , H E ⊥ C D , H F ⊥ S E
Ta có A B ⊥ S H K ⇒ S K H ⏜ = 60 °
Do đó S H = H K tan 60 °
Mặc khác H K = H B sin 60 ° ( Do Δ A B C là tam giác đều nên A B D ⏜ = 60 ° ) suy ra H K = a 3 sin 60 ° = a 3 6 ⇒ S H = a 2
Lại có H E = H D tan 60 ° = a 3 3 ⇒ H F = a 7 = d H ; S C D
Do đó B D H D = 3 2 ⇒ d B = 3 2 d H = 3 a 17 14

Chọn D.
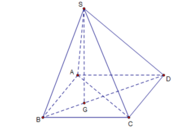
- Gọi G là trọng tâm tam giác ABC.
- Hình chóp S.ABC là hình chóp đều nên SG ⊥ (ABC).
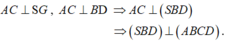
→ Góc giữa hai mặt phẳng (SBD) và (ABCD) bằng 90 °

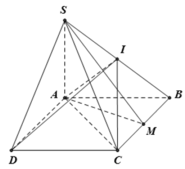
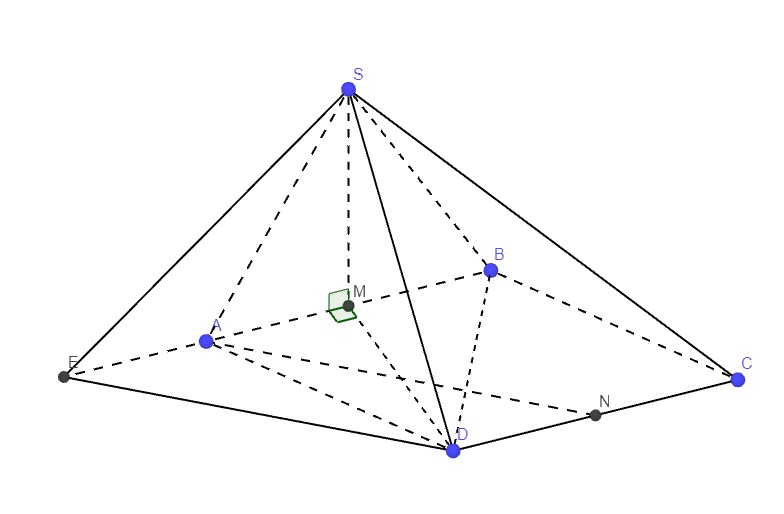
Gọi E là điểm đối xứng M qua A
\(\Rightarrow ANDE\) là hình bình hành (cặp cạnh đối AE và DN song song và bằng nhau)
\(\Rightarrow AN||DE\Rightarrow\) góc giữa AN và SD bằng góc giữa SD và DE
Do tam giác ABD đều \(\Rightarrow MD\perp AB\) \(\Rightarrow\Delta MDE\) vuông tại M
Do tam giác SAB đều \(\Rightarrow SM\perp AB\)
Mà \(\left(SAB\right)\perp\left(ABCD\right)\Rightarrow SM\perp\left(ABCD\right)\)
\(\Rightarrow\) Các tam giác SMD, SME vuông tại M
\(SM=\dfrac{AB\sqrt{3}}{2}=\dfrac{a\sqrt{3}}{2}\) (trung tuyến tam giác SAB đều)
\(MD=\dfrac{AB\sqrt{3}}{2}=\dfrac{a\sqrt{3}}{2}\) (trung tuyến tam giác ABD đều)
\(ME=2AM=AB=a\)
Pitago:
\(SD=\sqrt{SM^2+MD^2}=\dfrac{a\sqrt{6}}{2}\)
\(SE=\sqrt{SM^2+ME^2}=\dfrac{a\sqrt{7}}{2}\)
\(ED=\sqrt{MD^2+ME^2}=\dfrac{a\sqrt{7}}{2}\)
\(\Rightarrow cos\widehat{SDE}=\dfrac{SD^2+ED^2-SE^2}{2SD.ED}=\dfrac{\sqrt{42}}{14}\)

Đáp án C

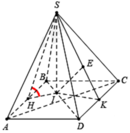
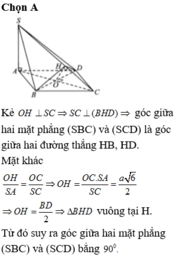
Gọi E và H lần lượt là hình chiếu của A lên CB và SE
Ta có: A E = A B sin A B E ^ = s i n 60 ° = a 3 2
A H = A E sin 60 ° = 3 2 a . 3 2 = 3 a 4


+) ABCD là hình thoi nên cũng là hình bình hành
Áp dụng quy tắc hình bình hành ta có:
\(\overrightarrow p = \overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {AC} \)
\(\Rightarrow |\overrightarrow p| = | \overrightarrow {AC}| =AC \)
+) \(\overrightarrow u = \overrightarrow {AB} - \overrightarrow {AD} = \overrightarrow {DB} \)
\(\Rightarrow |\overrightarrow u| = | \overrightarrow {DB}| =DB\)
+) \(\overrightarrow v = 2\overrightarrow {AB} - \overrightarrow {AC} = \overrightarrow {AB} + \left( {\overrightarrow {AB} - \overrightarrow {AC} } \right) = \overrightarrow {AB} + \overrightarrow {CB} \)\( = \overrightarrow {AB} + \overrightarrow {DA} = \overrightarrow {DB} \)
\(\Rightarrow |\overrightarrow v| = | \overrightarrow {DB}| =DB\)
+ Tính \(AC, DB\)
Tam giác ABD có \(AB=AD=a, \widehat A = 60^o\) nên nó là tam giác đều. Do đó DB = a.
Gọi O là giao điểm hai đường chéo.
Ta có: \(AO = AB. \sin B = a. \sin 60^o = \frac {a \sqrt 3}{2} \Rightarrow AC = a \sqrt 3\)
Vậy \(|\overrightarrow p| = a \sqrt 3 ,|\overrightarrow u| = a, |\overrightarrow v| = a.\)

* Ta có SA ⊥ (ABCD) nên AM là hình chiếu của SM trên mặt phẳng (ABCD)
![]()
* ΔABCcó AB = BC = a ( vì ABCD là hình thoi) và ![]() nên ΔABC đều.
nên ΔABC đều.
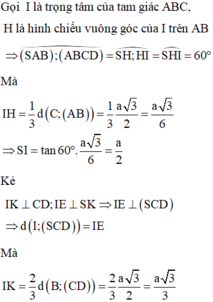
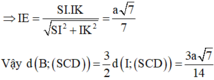
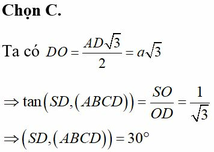

Trên tia đối của tia AD, lấy H sao cho AH=AD
=>A là trung điểm của HD
=>\(\overrightarrow{DA}=\overrightarrow{AH}\)
=>\(\left(\overrightarrow{AB};\overrightarrow{DA}\right)=\left(\overrightarrow{AB};\overrightarrow{AH}\right)=\widehat{BAH}\)
Ta có: ABCD là hình thoi
=>\(\widehat{BAD}+\widehat{ABC}=180^0\)
=>\(\widehat{BAD}=180^0-60^0=120^0\)
Ta có: \(\widehat{BAD}+\widehat{BAH}=180^0\)(hai góc kề bù)
=>\(\widehat{BAH}=180^0-120^0=60^0\)
=>\(\left(\overrightarrow{AB};\overrightarrow{DA}\right)=\widehat{BAH}=60^0\)