Cho 2 đoạn thẳng AB ; CD cắt nhau tại E . Các tia phân giác của các góc ACE và DBE cắt nhau ở K . Chứng minh rằng \(\widehat{BKC}\)= \(\widehat{\frac{BAC+\widehat{BDC}}{2}}\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

B1) Tỉ số của AB=11( vì 7+4)
Tỉ số của MA/AB=7/11
TỈ SỐ AB/MB= 11/4
B2) Độ dài đoạn AB= 10:2=5
Độ dài đoạn MB =10-5
k nhá
B1: Ta có: Tỉ số của AB là 11 ( = tỉ số MA + tỉ số MB)
=> tỉ số của MA/AB=7/11
tỉ số của AB/MB=11/4
B2: Độ dài của MA: 10/(2+3).2=4 cm
=> MB=AB-MA=10-4=6 cm
Chúc e hc tốt

Độ dài AM là:
\(6.\dfrac{2}{3}=4\) ( cm )
Vì N là trung điểm của MB nên
\(MN=NB=\dfrac{1}{2}MB=\dfrac{1}{2}.4=2\) ( cm )
\(\Rightarrow\)Độ dài AN là:
\(AM+MN=AN\)
Thay số: \(4+2=AN\\ \Rightarrow AN=6cm\).
Vậy \(AN=6cm\)

b: S=2+4+...+2^100
=>2S=2^2+2^3+...+2^101
=>S=2^101-2<2^101
a: Số đoạn thẳng tạo thành là \(C^2_{102}=5151\)


Từ giả thiết
CA/CB = 3/2
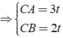 với t > 0
với t > 0
Nên AB = 10 cm = CA + CB = 5t ⇔ t = 2
Vậy CB = 4 cm

a: Ta có: I nằm giữa A và B
nên IA+IB=AB
=>IB=3cm
=>IA=IB
b: Vì I nằm giữa A và B
mà IA=IB
nên I là trung điểm của AB
Nối K với E.
Góc BKC = BKE + EKC
+) Trong tam giác CKE có: EKC = 180o - (KEC + ECK)
+) Trong tam giác BEK có: BKE = 180o - (KEB + EBK)
=> góc BKC = 360o - (KEC + ECK + KEB + EBK) (1)
Ta có: KEC + KEB = AEC + KEA + KEB = = AEC + 180o (2)
góc ECK + EBK = ACB2 +ABD2 =180o−(BAC+AEC)+180o−(BDC+DEB)2
=> góc ECK + EBK = 360o−(BAC+BDC)−2.AEC2 =180o−AEC−BAC+BDC2 (góc AEC = DEB vì đối đỉnh) (3)
Thay (2)(3) vào (1) ta được góc BKC = 360o−(360o−BAC+BDC2 )=BAC+BDC2
Thanks bạn nha