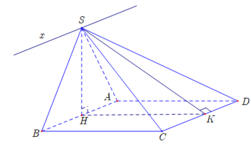
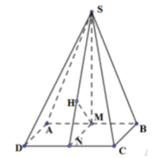
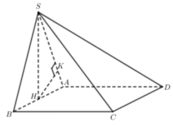
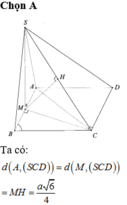
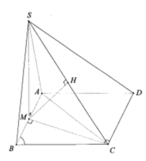
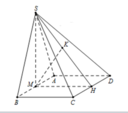
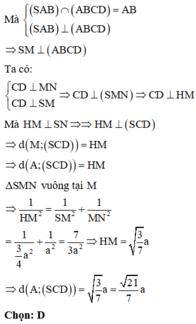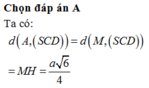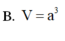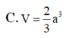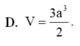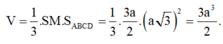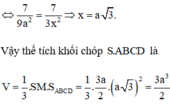Cho hình chóp S.ABCD có đáy là hình vuông cạnh 2a.Mặt bên SAB là tam giác đều và nằm trong mặt phẳng vuông góc với đáy.Gọi H là trung điểm AB.Tính khoảng cách từ C đến mặt phẳng (SHD)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Gợi ý xem bạn làm được ko, ko thì để mình trình bày luôn
Kẻ \(KC\perp HD;KC\cap HD=\left\{K\right\}\)
\(\left\{{}\begin{matrix}KC\perp HD\\KC\perp SH\end{matrix}\right.\Rightarrow KC\perp\left(SHD\right)\Rightarrow\left(SKC\right)\perp\left(SHD\right)\)
Kẻ \(CI\perp SK;CI\cap SK=\left\{I\right\}\Rightarrow CI\perp\left(SHD\right)\Rightarrow CI\perp\left(SHD\right)\)
\(\Rightarrow\left(SC,\left(SHD\right)\right)=\left(SC,SI\right)\)

Đáp án là B
Ta có: S H ⊥ A B ⇒ S H ⊥ A B C D .
Do A B / / C D ⇒ S A B ∩ S C D = S x / / A B . Mặt khác S H ⊥ C D S K ⊥ C D ⇒ S H ⊥ S x S K ⊥ S x
Suy ra góc giữa hai mặt phẳng S A B và S C D là góc giữa hai đường thẳng S H và S K .
Ta có: S H = 3 a 2 , H K = a . .
Xét tam giác S H K : tan H S K ^ = H K S H = 2 a a 3 = 2 3 3 .
Vậy tan α = 2 3 3 .