Vạch kẻ đường là:
A. Vạch chỉ phân chia làn đường, vị trí hướng đi, vị trí dừng lại B. Vị trí dừng và vị trí trên đường C. Vạch chỉ vị trí hướng đi và vị trí đứng D. A và B đúngHãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


câu 1 D:Cả A và B đều đúng
câu 2: D: A và B đúng
mik lm đại nên hok bik đúng hok, có j sai xin thứ lỗi

Bài này không khó đâu, cứ theo từng giai đoạn mà vẽ nhé.
a) Đồ thị biểu diễn quỹ đạo của tàu.
b) Tàu dừng lại tại vị trí P
Toạ độ của N là: \(x_N=14,1.\cos 45^0=10\) ; \(y_N=8+14,1.\cos45^0=18\),
Toạ độ của P là: \(x_P=x_N+5=15\) ; \(y_P=y_N=18\)
Vậy khoảng cách từ O đến nơi tàu dừng lại là: \(d=\sqrt{x_P^2+y_P^2}=\sqrt{15^2+18^2}\approx 23,43(km)\)
c) Theo câu B ta có toạ độ vị trí tàu dừng là \((15;18)\)

Áp dụng định lí cosin, ta có:
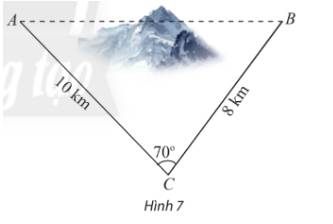
\(\begin{array}{l}A{B^2} = B{C^2} + A{C^2} - 2.BC.AC.\cos C\\ \Leftrightarrow A{B^2} = {8^2} + {10^2} - 2.8.10.\cos {70^o}\\ \Rightarrow AB \approx 10,45\end{array}\)
Vậy chiều dài tăng thêm vì không thể nối trực tiếp là:
\(AC + CB - AB = 10 + 8 - 10,45 = 7,55\;(km).\)

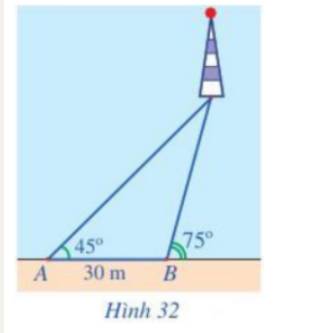
Gọi C là vị trí ngọn hải đăng và H là hình chiếu của C trên AB.
Khi đó CH là khoảng cách từ ngọn hải đăng tới bờ biển.
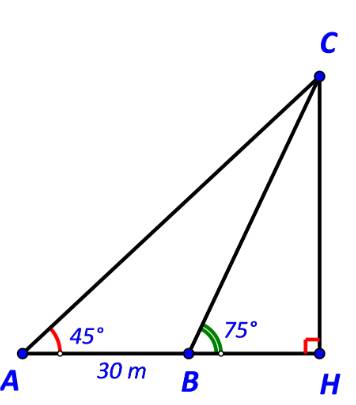
Ta có: \( \widehat {ACB} = \widehat {HBC} - \widehat {BAC} = {75^o} - {45^o} = {30^o}; \, \widehat {ABC} = {180^o} - {75^o} = {105^o}\)
Áp dụng định lí sin trong tam giác ABC ta có:
\(\frac{{AB}}{{\sin C}} = \frac{{AC}}{{\sin B}}\)
\( \Rightarrow AC = \sin B.\frac{{AB}}{{\sin C}} = \sin {105^o}.\frac{{30}}{{\sin {{30}^o}}} \approx 58\)
Tam giác ACH vuông tại H nên ta có:
\(CH = \sin A.AC = \sin {45^o}.58 \approx 41\)
Vậy ngọn hải đăng cách bờ biển 41 m.

a. Quãng đường từ nhà đến trường là: s = AB = 2 (km)
Độ dịch chuyển: d = AB = 2(km)
b. Quãng đường từ nhà đến trường rồi quay về hiệu sách là: s = AB + AB/2 = 3 (km)
Độ dịch chuyển: d = AB - AB/2 = 1 (km)
c. Quãng đường đi từ nhà đến hiệu sách rồi quay về là: s = AB/2 + AB/2 = 2 (km)
Độ dịch chuyển: d = AB/2 - AB/2 = 0 (km)
kết quả A
Đáp án:A
~Hok tốt~