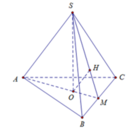
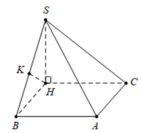
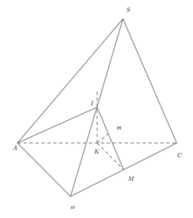
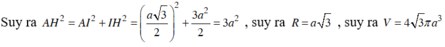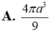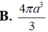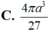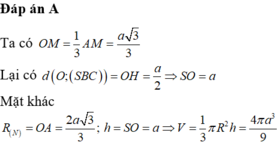Hình chóp S.ABC, đáy ABC là tam giác đều, Ol à trọng tâm ABC,H là trung diểm OA, SH vuông(ABC),SO=a,tam giác SAB vuông tại S.Tính thể tích hình chóp và khoảng cách từ tâm đường tròn ngoại tiếp tam giác SAC đến mặt (SOC)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


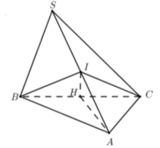
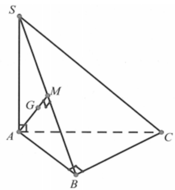
Gọi I là trung điểm của SA.
Tam giác SAB, SAC vuông tại B , C ⇒ I S = I A = I B = I C ⇒ I là tâm mặt cầu ngoại tiếp chóp S.ABC.
Gọi H là trung điểm của BC. Vì vuông tại là tâm đường tròn ngoại tiếp tam giác ABC.
⇒ I H ⊥ A B C .
Gọi R là bán kính mặt cầu ngoại tiếp chóp S.ABC. Theo bài ra ta có:

Xét tam giác vuông ABC có:
B C = A B 2 + A C 2 = 2 ⇒ A H = 1
Xét tam giác vuông IAH có:
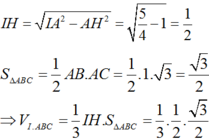
Ta có:
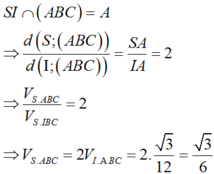
Xét tam giác vuông SAB có
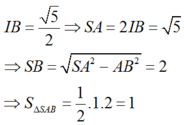
Ta có
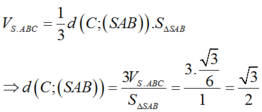
Chọn A.

Chọn đáp án D
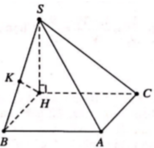
+ Gọi H là trung điểm SB. Do tam giác SAB vuông tại A, SBC vuông tại C suy ta HA = HB = HS = HC
Suy ra H là tâm mặt cầu.
+ Gọi I là hình chiếu của H lên (ABC). Do HA = HB = HC , suy ra IA = IB = IC
Suy ra I là trung điểm AC. Gọi P là trung điểm BC, do tam giác ABC vuông cân, suy ra
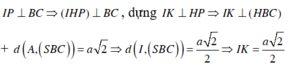
Áp dụng hệ thức
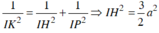
\