cho tam giác ABC có AB > AC . Từ trung điểm M của BC vẽ một đường thẳng vuông góc với tia phân giác của góc A, cắt tia phân giác tại H, cắt AB, AC lần lượt tại E VÀ F. chứng minh rằng :
a) BE=CF
b) AE=\(\frac{AB+AC}{2}\); BE=\(\frac{AB-AC}{2}\)
c) \(\widehat{BME}=\frac{\widehat{ACB}-\widehat{B}}{2}\)
GIUP MIK NHA !!!!!!!!!!

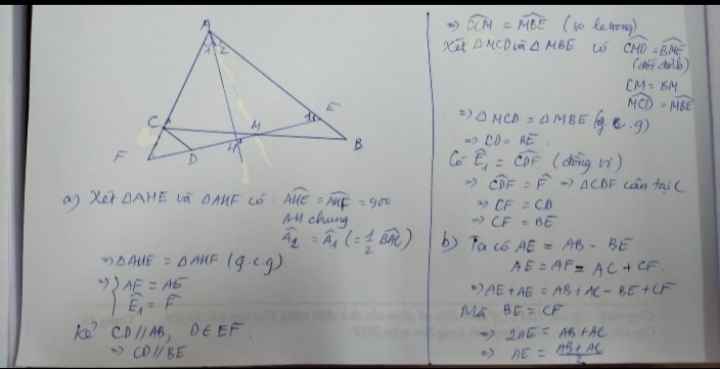


Bạn tự vẽ hình nha
a)_ Từ C kẻ đường thẳng song song với AB, cắt FE tại N => ^NCM = ^EBM (so le trong)
_Xét tg NCM và tg EBM ta có:
^NCM =^EBM(cmt)
CM=BM(gt)
^NMC =^EMB(đối đỉnh)
=> tg NCM = tg EBM (g.c.g)
=> CN = BE (2 cạnh tương ứng)
_CN // AB(cách vẽ) => ^CNF = ^AEF(đồng vị)(1)
Bạn c/m tg AHF = tg AHE(g.c.g)
=> ^AFH = ^AEH hay ^CFN = ^AEF(2)
(1),(2) => ^CNF = ^CFN => tg CFN cân tại C
=> CF = CN. Mà CN = BE(cmt) => CF = BE
b) _Ta có: AB = AE + BE; AC = AF - CF
=> AB + AC = AE+BE+AF-CF(*)
Tg AHF = tg AHE(cmt) => AF = AE
Lại có BE=CF(câu a) thay vào(*) ta có:
AB+AC = AE+BE+AE-BE =2.AE
=> AE=(AB+AC)/2
*Để mk nghĩ câu c đã