Bạn Dương có một bộ sưu tập gồm 169 đồng xu và muốn tặng bạn bè mỗi người một số đồng xu khác nhau,không có hai bạn nào nhận được số đồng xu bằng nhau.Hỏi nhiều nhất thì bạn Dương có thể tặng được cho bao nhiêu người bạn
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
24 tháng 2 2018
quy về bài toán x số nguoi nhận x ; x thuộc N
1+2+3+....+x <= 169 tim max x
\(\dfrac{x\left(x+1\right)}{2}\le169\)
có x =17 <=> 17.9=153
có x =18 <=> 9.19=171
153 <169 <171
vậy x =17 là lớn nhất
22 tháng 2 2016
Lấy ra 10 đồng xu, lật ngược hết 10 đồng xu đó sẽ có được số đồng sấp bằng với nhóm 90 đồng xu kia. Có thể đặt x là số xu sấp trong nhóm 90 xu sau khi chia làm 2 nhóm, số xu sấp ở nhóm 10 xu sẽ là 10-x, vậy nên khi lật ngược hết nhóm 10 xu, số xu sấp bên đó sẽ là x và bằng với số xu sấp trong nhóm 90 xu
HQ
Hà Quang Minh
Giáo viên
8 tháng 10 2023
a)
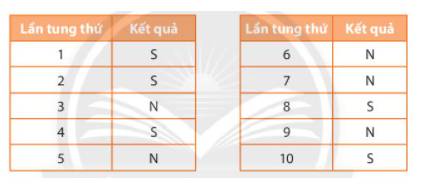
- Bạn Hùng đã tung đồng xu 10 lần. Kết quả của lần thứ nhất là mặt sấp, lần thứ năm là mặt ngửa.
- Có 2 kết quả khác nhau có thể xảy ra, đó là kết quả đồng xu hiện ra mặt sấp hoặc đồng xu hiện ra mặt ngửa.
b)
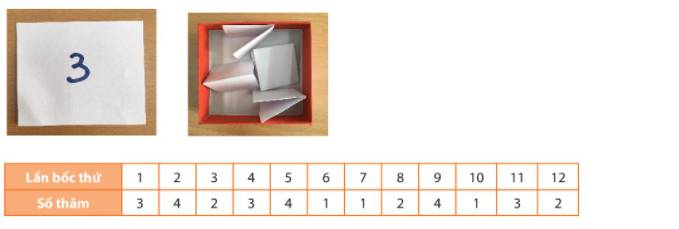
- Kết quả lần thứ 5 là số 4, lần thứ 6 là số 1.
- Có 4 kết quả khác nhau có thể xảy ra, đó là các kết quả 1,2,3,4.
giả sử bạn Dương tặng được nhiều nhất cho k người
gọi x_k là số đồng xu bạn dương tặng cho người thứ k theo thứ tự từ ít đến nhiều đồng xu nhất
nên ta có :
\(x_1< x_2< x_3< ..< x_k\)
cụ thể hơn ta có : \(x_i+1\le x_{i+1}\)
mà ta có : \(x_1+x_2+..+x_k=169\ge x_1+x_1+1+x_1+2+..+x_1+k-1=kx_1+\frac{k\left(k-1\right)}{2}\ge k+\frac{k\left(k-1\right)}{2}\)
hay ta có : \(k^2+k\le338\Rightarrow k\le17\)
vậy tối đa Dương tặng được cho 17 người