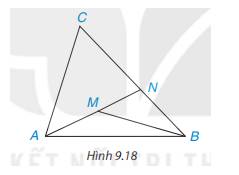
Cho tam giác ABC. Hai điểm phân biệt M, N thay đổi sao cho MA/NA=MB/NB=MB/NC khác 1 . Chứng minh rằng đường thẳng MN đi qua một điểm cố định.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) 3 điểm M,N,B không thẳng hàng.
Áp dụng bất đẳng thức tam giác trong tam giác MNB có:
MB < MN + NB
MA + MB < MA + MN + NB
MA + MB < NA + NB ( vì MA + MN = NA) (1)
b) 3 điểm A,N,C không thẳng hàng.
Áp dụng bất đẳng thức tam giác trong tam giác ACN có:
NA < CA + CN
NA + NB < CA + CN + NB
NA + NB < CA + CB ( vì CN + NB = CB) (2)
c) Từ (1) và (2) ta có:
MA + MB < NA + NB < CA + CB
Vậy MA + MB < CA + CB

a) \(2\overrightarrow{IA}-\overrightarrow{IB}+\overrightarrow{IC}=\overrightarrow{0}\Rightarrow2\overrightarrow{IA}-\overrightarrow{IA}-\overrightarrow{AB}+\overrightarrow{IA}+\overrightarrow{AC}=\overrightarrow{0}\)
\(\Rightarrow2\overrightarrow{AI}=\overrightarrow{AC}-\overrightarrow{AB}\Rightarrow\overrightarrow{AB}+2\overrightarrow{AI}=\overrightarrow{AC}\). Từ đó suy ra cách dựng điểm I:
b) Với cách lấy điểm I như trên, ta có điểm I cố định. Khi đó MN đi qua I, thật vậy:
\(\overrightarrow{MN}=2\overrightarrow{MA}-\overrightarrow{MB}+\overrightarrow{MC}=2\overrightarrow{MI}+2\overrightarrow{IA}-\overrightarrow{MI}-\overrightarrow{IB}+\overrightarrow{MI}+\overrightarrow{IC}\)
\(=2\overrightarrow{MI}+\left(2\overrightarrow{IA}-\overrightarrow{IB}+\overrightarrow{IC}\right)=2\overrightarrow{MI}\)
Suy ra I là trung điểm MN hay MN đi qua điểm I cố định (đpcm).
c) \(\overrightarrow{MP}=\frac{1}{2}\overrightarrow{MB}+\frac{1}{2}\overrightarrow{MN}=\overrightarrow{MA}+\frac{1}{2}\overrightarrow{MC}\)
Đặt K là điểm sao cho \(\overrightarrow{KA}+\frac{1}{2}\overrightarrow{KC}=\overrightarrow{0}\Rightarrow\hept{\begin{cases}K\in\left[AC\right]\\KA=\frac{1}{2}KC\end{cases}}\)tức K xác định
Khi đó \(\overrightarrow{MP}=\overrightarrow{MK}+\overrightarrow{KA}+\frac{1}{2}\overrightarrow{MK}+\frac{1}{2}\overrightarrow{KC}=\frac{3}{2}\overrightarrow{MK}\), suy ra MP đi qua K cố định (đpcm).
có ai làm được chưa vậy ạ