2

a)

d đi qua A (1;2), B(2;5)

=> Ta có hệ phương trình: \(\left\{{}\begin{matrix}\left(m-1\right).1+n=2\\\left(m-1\right).2+n=5\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}m+n=3\\2m+n=7\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m=4\\n=-1\end{matrix}\right.\)

b)

d có hệ số góc a = 3 => d: y = 3x + n

=> m -1 = 3 <=> m = 4

d cắt Ox tại x = -2, y = 0 \(\Leftrightarrow0=3.\left(-2\right)+n\) => n = 6

c)

d trùng d' \(\Rightarrow\left\{{}\begin{matrix}m-1=5\\n=-3\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}m=6\\n=-3\end{matrix}\right.\)

Đường thẳng d có hệ số góc bằng 4 ↔ a - 2 = 4 ↔ a = 6

Mặt khác (d) đi qua điểm M (1;-3) nên thay a = 6, x = 1; y = -3 vào y = (a - 2)x + b.

Khi đó ta có: -3 = (6 - 2).1 + b

→ -3 = 4 + b

→ b = -7

Vậy a = 6 và b = -7 là các giá trị cần tìm và khi đó (d): y = 4x - 7

a) Gọi pt đường thẳng (d) là : \(y=ax+b\left(a\ne0\right)\)

Vì (d) có hệ số góc là 2 \(\Rightarrow a=2\Rightarrow y=2x+b\)

Vì đường thẳng d đi qua điểm \(M\left(-1;3\right)\)

\(\Rightarrow3=-2+b\Rightarrow b=5\Rightarrow y=2x+5\)

b) Gọi pt đường thẳng d là \(y=ax+b\left(a\ne0\right)\)

Vì \((d)\parallel (d')\Rightarrow a=2\Rightarrow y=2x+b\)

Vì đường thẳng d đi qua điểm \(M\left(3;5\right)\)

\(\Rightarrow5=6+b\Rightarrow b=-1\Rightarrow y=2x-1\)

cho/mình/hỏi/bài/này/phải/vẽ/hình/ko/ạ

Bài 3 làm sao v ạ?

Đường thẳng d đi qua A và có hệ số góc k nên có dạng y= k( x+ 1)   hay

Kx- y+k=0 .

Phương trình hoành độ giao điểm của C  và  d là:

x 3 - 3 x 2 + 4 = k x + k ⇔ ( x + 1 ) ( x 2 - 4 x + 4 - k ) = 0

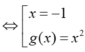
D cắt tại ba điểm phân biệt khi phương trình (*) có hai nghiệm phân biệt khác -1

⇔ ∆ ' > 0 g ( - 1 ) ≠ 0 ⇔ k > 0 k ≠   9

Khi đó g( x) =0 khi x=2- k ;   x = 2 + k    Vậy các giao điểm của hai đồ thị lần lượt là

A ( - 1 ;   0 ) ; B ( 2 - k ;   3 k - k k ) ; C ( 2 + k ;   3 k + k k ) .

Tính được

B C = 2 k 1 + k 2 , d ( O , B C ) = d ( O , d ) = k 1 + k 2 .

Khi đó 

S ∆ O B C = 1 2 . k k 2 + 1 . 2 k . k 2 + 1 = 1 ⇔ k k = 1 ⇔ k 3 = 1 ⇔ k = 1 .

Vậy k= 1 thỏa yêu cầu bài toán.

Chọn C.