Cho đường tròn và điểm M ở ngoài đường tròn với OM >2R. Vẽ hai tiếp tuyến MA, MB và đường kính AD của đường tròn(O) (A, B là các tiếp điểm).Gọi C là giao điểm của MD với đường tròn(O) , H là giao điểm MO với AB . a)cm H là trung điểm AB. b)cm AC vuông góc với MD và tứ giác AHCM nội tiếp c)cm góc AMC= 1/2 góc CHD. d)gọi K là giao điểm MD với AB , I là giao điểm của BC với MH. cm 3...
Đọc tiếp
Cho đường tròn và điểm M ở ngoài đường tròn với OM >2R. Vẽ hai tiếp tuyến MA, MB và đường kính AD của đường tròn(O) (A, B là các tiếp điểm).Gọi C là giao điểm của MD với đường tròn(O) , H là giao điểm MO với AB . a)cm H là trung điểm AB. b)cm AC vuông góc với MD và tứ giác AHCM nội tiếp c)cm góc AMC= 1/2 góc CHD. d)gọi K là giao điểm MD với AB , I là giao điểm của BC với MH. cm 3 đường thẳng MB, IK, và HD đồng quy. Mấy bạn giải giúp mình nha, cảm ơn các bạn lắm
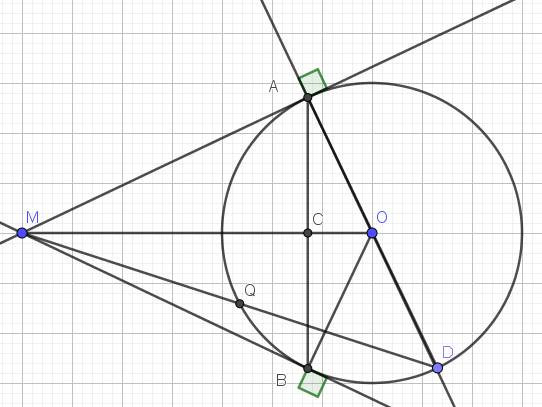
a) Áp dụng tính chất 2 tiếp tuyến giao nhau thì MA = MB. Do đó OM là trung trực đoạn AB.
Vì OM giao AB tại H nên H là trung điểm của AB (đpcm).
b) Ta thấy ^ABD chắn nửa đường tròn (O) nên BD vuông góc với AB, có AB vuông góc OM
=> BD // OM => ^HMC = ^BDC (So le trong) = ^HAC => 4 điểm A,H,C,M cùng thuộc 1 đường tròn
Hay tứ giác AHCM nội tiếp (đpcm).
c) Áp dụng hệ thức lượng ta có MC.MD = MH.MO (= MB2) => Tứ giác DOHC nội tiếp
Vì ^ODC = ^OCD nên ^HO là phân giác ngoài của ^CHD. Lai có HO vuông góc HB
Suy ra HB là phân giác ^CHD => ^CHD = 2.^BHC = 2.AMC (Do tứ giác AHCM nội tiếp) (đpcm).
d) Bổ đề: Xét hình thang ABCD (AB // CD) có AC cắt BD tại O, M là trung điểm CD. Khi đó AD,BC,MO đồng quy.
Thật vậy: Gọi AD cắt BC tại S. Ta có \(\frac{OA}{OC}=\frac{AB}{CD}=\frac{SA}{SD}\). Từ đó: \(\frac{OA}{OC}.\frac{MC}{MD}.\frac{SD}{SA}=1\)
Theo ĐL Melelaus cho \(\Delta\)ACD thì 3 điểm M,O,S thẳng hàng. Tức là BC,AD,MO cắt nhau tại S.
Giải bài toán: Có ^HCB = ^HCK + ^BCD = ^HAM + ^BAD = ^MAO = 900 => HC vuông góc BI
Áp dụng hệ thức lượng trong tam giác vuông: IH2 = IB.IC
Mặt khác dễ thấy ^IMC= ^BDC = ^IBM => \(\Delta\)CIM ~ \(\Delta\)MIB (g.g) => IM2 = IB.IC
Suy ra IH = IM. Lúc đó, xét hình thang BDHM (HM // BD), MD cắt BH tại K, I là trung điểm HM
Ta thu được MB,HD,IK đồng quy (Theo bổ đề) (đpcm).