
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


1) PT \(\Leftrightarrow\left(\dfrac{x+1}{35}+1\right)+\left(\dfrac{x+3}{33}+1\right)=\left(\dfrac{x+5}{31}+1\right)+\left(\dfrac{x+7}{29}+1\right)\)
\(\Leftrightarrow\dfrac{x+36}{35}+\dfrac{x+36}{33}=\dfrac{x+36}{31}+\dfrac{x+36}{29}\)
\(\Leftrightarrow\left(x+36\right)\left(\dfrac{1}{29}+\dfrac{1}{31}-\dfrac{1}{33}-\dfrac{1}{35}\right)=0\)
\(\Leftrightarrow x+36=0\) (Do \(\dfrac{1}{29}+\dfrac{1}{31}-\dfrac{1}{33}-\dfrac{1}{35}>0\))
\(\Leftrightarrow x=-36\).
Vậy nghiệm của pt là x = -36.
2) x(x+1)(x+2)(x+3)= 24
⇔ x.(x+3) . (x+2).(x+1) = 24
⇔(\(x^2\) + 3x) . (\(x^2\) + 3x + 2) = 24
Đặt \(x^2\)+ 3x = b
⇒ b . (b+2)= 24
Hay: \(b^2\) +2b = 24
⇔\(b^2\) + 2b + 1 = 25
⇔\(\left(b+1\right)^2\)= 25
+ Xét b+1 = 5 ⇒ b=4 ⇒ \(x^2\)+ 3x = 4 ⇒ \(x^2\)+4x-x-4=0 ⇒x(x+4)-(x+4)=0
⇒(x-1)(x+4)=0⇒x=1 và x=-4
+ Xét b+1 = -5 ⇒ b=-6 ⇒ \(x^2\)+3x=-6 ⇒\(x^2\) + 3x + 6=0
⇒\(x^2\) + 2.x.\(\dfrac{3}{2}\) + (\(\dfrac{3}{2}\))2 = - \(\dfrac{15}{4}\) Hay ( \(x^2\) +\(\dfrac{3}{2}\) )2= -\(\dfrac{15}{4}\) (vô lí)
⇒x= 1 và x= 4

a) Ta có: \(\dfrac{AE}{AB}=\dfrac{2}{5}\)
\(\dfrac{AF}{AC}=\dfrac{4}{10}=\dfrac{2}{5}\)
Do đó: \(\dfrac{AE}{AB}=\dfrac{AF}{AC}\)\(\left(=\dfrac{2}{5}\right)\)
Xét ΔAEF và ΔABC có
\(\dfrac{AE}{AB}=\dfrac{AF}{AC}\)(cmt)
\(\widehat{A}\) chung
Do đó: ΔAEF\(\sim\)ΔABC(c-g-c)
Suy ra: \(\dfrac{AE}{AB}=\dfrac{EF}{BC}\)(Các cặp cạnh tương ứng tỉ lệ)
\(\Leftrightarrow\dfrac{2}{5}=\dfrac{EF}{12}\)
hay EF=4,8(cm)
Vậy: EF=4,8cm

x3 _ x2 _ 4x - 4 = 0
x mũ 2(x+1)- 4(x+1)=0
(x mũ 2 - 4) (x+1)=0
(x+2) (x-2) (x+1) =0
suy ra (x+2)=0
(x-2)=0
(x+1)=0
vậy x=-2
x=2
x= -1
good luck!
Sửa đề : \(x^3-x^2-4x+4=0\)
\(\Leftrightarrow x^2\left(x-1\right)-4\left(x-1\right)=0\)
\(\Leftrightarrow\left(x^2-4\right)\left(x-1\right)=0\)
\(\Leftrightarrow\left(x-2\right)\left(x+2\right)\left(x-1\right)=0\Leftrightarrow x=\pm2;1\)

$P=4a^2+4a(b-3)+b^2-6b+9+3b^2-6b+3$
$=4a^2+2.2a.(b-3)+(b-3)^2+3.(b-1)^2$
$=(2a+b-3)^2+3.(b-1)^2$
Mà $(2a+b-3)^2 \geq 0;3.(b-1)^2 \geq 0$ với mọi $a;b$
Nên $P=(2a+b-3)^2+3.(b-1)^2 \geq 0$
Dấu $=$ xảy ra $⇔(2a+b-3)^2=0;3.(b-1)^2=0⇔2a+b-3=0;b=1⇔a=1;b=1$
Vậy $MinP=0$ tại $a=b=1$

a) Xét ΔAEB vuông tại E và ΔAFC vuông tại F có
\(\widehat{FAC}\) chung
Do đó: ΔAEB∼ΔAFC(g-g)
b) Ta có: ΔAEB∼ΔAFC(cmt)
nên \(\dfrac{AE}{AF}=\dfrac{AB}{AC}\)(Các cặp cạnh tương ứng tỉ lệ)
hay \(\dfrac{AE}{AB}=\dfrac{AF}{AC}\)
Xét ΔAEF và ΔABC có
\(\dfrac{AE}{AB}=\dfrac{AF}{AC}\)(cmt)
\(\widehat{BAC}\) chung
Do đó: ΔAEF∼ΔABC(c-g-c)

a) (Bạn tự vẽ hình ạ)
Ta có AD.AB = AE.AC
⇒ \(\dfrac{AD}{AC}=\dfrac{AE}{AB}\)
Xét \(\Delta ABC\) và \(\Delta AED\) có:
\(\dfrac{AD}{AC}=\dfrac{AE}{AB}\)
\(\widehat{A}:chung\)
⇒ \(\Delta ABC\sim\Delta AED\) \(\left(c.g.c\right)\)
⇒ DE // BC


a) Xét ΔAHB vuông tại H và ΔDAB vuông tại A có
\(\widehat{ABH}\) chung
Do đó: ΔAHB∼ΔDAB(g-g)

Lời giải:
Vận tốc trung bình đi từ A đến B là:
$\frac{20+30}{2}=25$ (km/h)
Kiến thức cần nhớ:
Vận tốc trung bình bằng tổng quãng đường chia cho tổng thời gian đi hết quãng đường đó!
Công thức Vtb = \(\dfrac{S_1+S_2+...+S_n}{t_1+t_2+...+t_n}\)
Giải chi tiết:
Gọi quãng đường AB là: S (km); S > 0
Thời gian người đó đi hết nửa quãng đường đầu là:
\(\dfrac{S}{2}\) : 20 = \(\dfrac{S}{40}\) (giờ)
Thời gian người đó đi hết nửa quãng đường sau là:
\(\dfrac{S}{2}\) : 30 = \(\dfrac{S}{60}\) (giờ)
Vận tốc trung bình của người đó đi từ A đến B là:
Áp dụng công thức Vtb = \(\dfrac{S_1+S_2}{t_1+t_2}\) ta có
Vtb = \(\dfrac{S}{\dfrac{S}{40}+\dfrac{S}{60}}\)
Vtb = \(\dfrac{S}{S.\left(\dfrac{1}{40}+\dfrac{1}{60}\right)}\)
Vtb = \(\dfrac{1}{\dfrac{1}{24}}\)
Vtb = 24 (km/h)
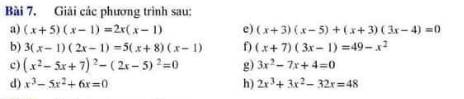


a: \(\left(x+5\right)\left(x-1\right)=2x\left(x-1\right)\)
=>\(2x\left(x-1\right)-\left(x+5\right)\left(x-1\right)=0\)
=>\(\left(x-1\right)\left(2x-x-5\right)=0\)
=>(x-1)(x-5)=0
=>\(\left[{}\begin{matrix}x=1\\x=5\end{matrix}\right.\)
b: \(3\left(x-1\right)\left(2x-1\right)=5\left(x+8\right)\left(x-1\right)\)
=>\(\left(x-1\right)\left(6x-3\right)-\left(x-1\right)\left(5x+40\right)=0\)
=>\(\left(x-1\right)\left(6x-3-5x-40\right)=0\)
=>(x-1)(x-43)=0
=>\(\left[{}\begin{matrix}x=1\\x=43\end{matrix}\right.\)
c: \(\left(x^2-5x+7\right)^2-\left(2x-5\right)^2=0\)
=>\(\left(x^2-5x+7-2x+5\right)\left(x^2-5x+7+2x-5\right)=0\)
=>\(\left(x^2-7x+12\right)\left(x^2-3x+2\right)=0\)
=>(x-3)(x-4)(x-1)(x-2)=0
=>\(\left[{}\begin{matrix}x=3\\x=4\\x=1\\x=2\end{matrix}\right.\)
d: \(x^3-5x^2+6x=0\)
=>\(x\left(x^2-5x+6\right)=0\)
=>x(x-2)(x-3)=0
=>\(\left[{}\begin{matrix}x=0\\x=2\\x=3\end{matrix}\right.\)
e: \(\left(x+3\right)\left(x-5\right)+\left(x+3\right)\left(3x-4\right)=0\)
=>(x+3)(x-5+3x-4)=0
=>(x+3)(4x-9)=0
=>\(\left[{}\begin{matrix}x=-3\\x=\dfrac{9}{4}\end{matrix}\right.\)
f: \(\left(x+7\right)\left(3x-1\right)=49-x^2\)
=>\(\left(x+7\right)\left(3x-1\right)+x^2-49=0\)
=>(x+7)(3x-1)+(x-7)(x+7)=0
=>(x+7)(3x-1+x-7)=0
=>(x+7)(4x-8)=0
=>\(\left[{}\begin{matrix}x=-7\\x=2\end{matrix}\right.\)
g: \(3x^2-7x+4=0\)
=>\(3x^2-3x-4x+4=0\)
=>(x-1)(3x-4)=0
=>\(\left[{}\begin{matrix}x=1\\x=\dfrac{4}{3}\end{matrix}\right.\)
h: \(2x^3+3x^2-32x=48\)
=>\(2x^3+3x^2-32x-48=0\)
=>\(x^2\left(2x+3\right)-16\left(2x+3\right)=0\)
=>\(\left(2x+3\right)\left(x^2-16\right)=0\)
=>(2x+3)(x-4)(x+4)=0
=>\(\left[{}\begin{matrix}x=-\dfrac{3}{2}\\x=4\\x=-4\end{matrix}\right.\)
a) (x + 5)(x - 1) = 2x(x - 1)
(x + 5)(x - 1) - 2x(x - 1) = 0
(x - 1)(x + 5 - 2x) = 0
(x - 1)(5 - x) = 0
x - 1 = 0 hoặc 5 - x = 0
*) x - 1 = 0
x = 1
*) 5 - x = 0
x = 5
Vậy S = {1; 5}
b) 3(x - 1)(2x - 1) = 5(x + 8)(x - 1)
(x - 1)(6x - 3) = (5x + 40)(x - 1)
(x - 1)(6x - 3) - (5x + 40)(x - 1) = 0
(x - 1)(6x - 3 - 5x - 40) = 0
(x - 1)(x - 43) = 0
x - 1 = 0 hoặc x - 43 = 0
*) x - 1 = 0
x = 1
*) x - 43 = 0
x = 43
Vậy S = {1; 43}
c) (x² - 5x + 7)² - (2x - 5)² = 0
(x² - 5x + 7 - 2x + 5)(x² - 5x + 7 + 2x - 5) = 0
(x² - 7x + 12)(x² - 3x + 2) = 0
x² - 7x + 12 = 0 hoặc x² - 3x + 2 = 0
*) x² - 7x + 12 = 0
x² - 3x - 4x + 12 = 0
(x² - 3x) - (4x + 12) = 0
x(x - 3) - 4(x - 3) = 0
(x - 3)(x - 4) = 0
x - 3 = 0 hoặc x - 4 = 0
+) x - 3 = 0
x = 3
+) x - 4 = 0
x = 4
*) x² - 3x + 2 = 0
x² - x - 2x + 2 = 0
(x² - x) - (2x - 2) = 0
x(x - 1) - 2(x - 1) = 0
(x - 1)(x - 2) = 0
x - 1 = 0 hoặc x - 2 = 0
+) x - 1 = 0
x = 1
+) x - 2 = 0
x = 2
Vậy S = {1; 2; 3; 4}
d) x³ - 5x² + 6x = 0
x(x² - 5x + 6) = 0
x = 0 hoặc x² - 5x + 6 = 0
*) x² - 5x + 6 = 0
x² - 2x - 3x + 6 = 0
(x² - 2x) - (3x - 6) = 0
x(x - 2) - 3(x - 2) = 0
(x - 2)(x - 3) = 0
x - 2 = 0 hoặc x - 3 = 0
+) x - 2 = 0
x = 2
+) x - 3 = 0
x = 3
Vậy S = {0; 2; 3}