Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

b: \(\Leftrightarrow3n^3+n^2+9n^2+3n-3n-1-4⋮3n+1\)
\(\Leftrightarrow3n+1\in\left\{1;-1;2;-2;4;-4\right\}\)
\(\Leftrightarrow n\in\left\{0;-1;1\right\}\)

\(x^4-x^3+6x^2-x+a=x^2\left(x^2-x+5\right)+x^2-x+a\)
Do \(x^2\left(x^2-x+5\right)\) chia hết \(x^2-x+5\)
\(\Rightarrow x^2-x+a\) chia hết \(x^2-x+5\)
\(\Rightarrow a=5\)

\(a,n^3-2n^2+3n+3=n^3-n^2-n^2+n+2n-2+5\\ =\left(n-1\right)\left(n^2-n+2\right)+5\\ \Leftrightarrow n^3-2n^2+3n+3⋮\left(n-1\right)\\ \Leftrightarrow5⋮n-1\\ \Leftrightarrow n-1\in\left\{-5;-1;1;5\right\}\\ \Leftrightarrow n\in\left\{-4;0;2;6\right\}\)
\(b,\Leftrightarrow x^4+6x^3+7x^2-6x+a\\ =x^4+3x^3-x^2+3x^3+9x^2-3x-x^2-3x+1-1+a\\ =\left(x^2+3x-1\right)\left(x^2+3x-1\right)-1+a\\ =\left(x^2+3x-1\right)^2+a-1\)
Để \(x^4+6x^3+7x^2-6x+a⋮x^2+3x-1\)
\(\Leftrightarrow a-1=0\Leftrightarrow a=1\)

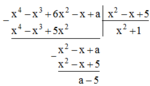
Để có phép chia hết thì số dư phải bằng 0.
Ta có: a – 5 = 0 hay a = 5.

Đặt \(f\left(x\right)=2x^3-3x^2+x+a\)
Ta có: phép chia \(f\left(x\right)\) cho \(x+2\) có dư là \(R=f\left(-2\right)\)
\(\Rightarrow f\left(-2\right)=2.\left(-2\right)^3-3.\left(-2\right)^2+\left(-2\right)+a\)
\(f\left(-2\right)=2.\left(-8\right)-3.4-2+a\)
\(f\left(-2\right)=-16-12-2+a\)
\(f\left(-2\right)=-20+a\)
Để \(f\left(x\right)\) chia hết cho \(x+2\) thì \(R=0\) hay \(f\left(-2\right)=0\)
\(\Rightarrow-20+a=0\Leftrightarrow a=20\)

A(x)=(1-x^n)(1+x^n)/(1-x)(1+x)
B(x)=1-x^n/1-x
A(x) chia hết cho B(x) khi 1-x^n chia hết cho 1+x
x^n+1/x+1=A(x)+(1+(-1)^n)/(x+1)
=>1-x^n chia hết cho 1+x khi và chỉ khi n=2k+1

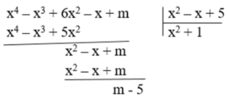
1. Ta có : A = a2 + 2ab + 50 - 12a - 12b + b2
= ( a2 + 2ab + b2 ) - ( 12a + 12b ) + 50
= ( a + b )2 - 12( a + b ) + 50
= 22 - 12.2 + 50
= 30
2. Đặt f(x) = x4 - x3 + 6x2 - x + n
g(x) = x2 - x + 5
Đặt thương trong phép chia f(x) cho g(x) là h(x)
f(x) bậc 4 ; g(x) bậc 2 => h(x) bậc 2
=> h(x) có dạng x2 + ax + b
Khi đó : f(x) chia hết cho g(x) <=> f(x) = g(x).h(x)
<=> x4 - x3 + 6x2 - x + n = ( x2 - x + 5 )( x2 + ax + b )
<=> x4 - x3 + 6x2 - x + n = x4 + ax3 + bx2 - x3 - ax2 - bx + 5x2 + 5ax + 5b
<=> x4 - x3 + 6x2 - x + n = x4 + ( a - 1 )x3 + ( b - a + 5 )x2 + ( 5a - b )x + 5b
Đồng nhất hệ số ta có :
a - 1 = -1 ; b - a + 5 = 6 ; 5a - b = -1 ; 5b = n
=> a = 0 ; b = 1 ; n = 5
=> n = 5
Vậy n = 5
Còn có cách khác
Thực hiện phép chia đa thức: x4 - x3 + 6x2 - x +n chia cho đa thức x2 - x + 5 có thương x2 + 1 phần dư là n - 5
Để đa thức x4 - x3 + 6x2 - x +n chia hết cho đa thức x2 - x + 5 => n - 5 = 0
=> n = 5
Tuy nhiên đề đúng là đa thức x4 - x2 + 6x2 - x +n hay đa thức x4 - x3 + 6x2 - x +n ?