Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

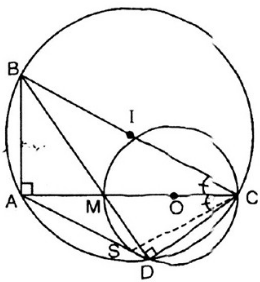
a, ta có ^BAC=900(góc nội tiếp chắn nửa đường tròn đường kính BC)
^MDC=900(góc nội tiếp chắn nửa đường tròn đường kính MC)
=>^BAC=^MDC(=900)
=>tứ giác ABCD nội tiếp (hai đỉnh A và D kề nhau cùng nhìn cạnh BC dưới hai góc bằng nhau)
b. vì tứ giác ABCD nội tiếp (câu a) nên ^ABD=^ACD (hai góc nội tiếp cùng chắn cung AD)
c, ta có bốn điểm D,S,C,M cùng thuộc đường tròn đường kính MC
=>tứ giác DSCM nội tiếp
=>^ADM=^SCM (cùng bù với ^MDS)
Mà ADCB nội tiếp nên ^ADM=^MCB( hai góc nội tiếp cùng chắn cung AB)
Do đó ^SCM=^MCB
=>CA là tia phân giác ^SCB

a) Ta có: \(\sin\widehat{ACB}=\dfrac{AB}{BC}\)
nên \(AB=\dfrac{3}{5}\cdot20=12\left(cm\right)\)
Xét ΔABC vuông tại A có
\(AB^2+AC^2=BC^2\)
\(\Leftrightarrow AC^2=20^2-12^2=256\)
hay AC=16(cm)
b) Áp dụng hệ thức lượng trong tam giác vuông vào ΔCBD vuông tại B có BA là đường cao ứng với cạnh huyền CD, ta được:
\(AC\cdot AD=AB^2\)(1)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(BH\cdot BC=AB^2\)(2)
Từ (1) và (2) suy ra \(AC\cdot AD=BH\cdot BC\)