Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài 1:
Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow AC^2=15^2-9^2=144\)
hay AC=12(cm)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(\left\{{}\begin{matrix}AB^2=BH\cdot BC\\AC^2=CH\cdot BC\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}BH=\dfrac{9^2}{15}=\dfrac{81}{15}=5.4\left(cm\right)\\CH=\dfrac{12^2}{15}=\dfrac{144}{15}=9,6\left(cm\right)\end{matrix}\right.\)
Áp dụng định lí Pytago vào ΔAHB vuông tại H, ta được:
\(AH^2+HB^2=AB^2\)
\(\Leftrightarrow AH^2=9^2-5.4^2=51,84\)
hay AH=7,2(cm)

Áp dụng định lí pi ta go
=> AB2 + AC2 = 289
Mà \(\dfrac{AB}{AC}\) = \(\dfrac{8}{15}\)=> (\(\dfrac{AB}{AC}\))2 = \(\dfrac{64}{225}\)
=> AC2=225 => AC = 15 => AB = 8
Ta có: AB.AC=BC . AH
=> AH = 120/17=7.06
=>BH = 3.76
=> CH = 13.24
Đúng thì like giúp mik nha bạn. Thx bạn

Bài 5:
Ta có: \(AB^2=BH\cdot BC\)
\(\Leftrightarrow BH\left(BH+9\right)=400\)
\(\Leftrightarrow BH^2+25HB-16HB-400=0\)
\(\Leftrightarrow BH=16\left(cm\right)\)
hay BC=25(cm)
Xét ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC
nên \(\left\{{}\begin{matrix}AC^2=CH\cdot BC\\AH\cdot BC=AB\cdot AC\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}AC=15\left(cm\right)\\AH=12\left(cm\right)\end{matrix}\right.\)

Ta có: BC=BH+CH
nên BC=25(cm)
Xét ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC
nên \(\left\{{}\begin{matrix}AB^2=BH\cdot BC\\AC^2=CH\cdot BC\\AH\cdot BC=AB\cdot AC\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}AB=15\left(cm\right)\\AC=20\left(cm\right)\\AH=12\left(cm\right)\end{matrix}\right.\)

Vì AM là trung tuyến ứng với cạnh huyền BC nên \(AM=\dfrac{1}{2}BC=7,5\left(cm\right)\)
Áp dụng PTG: \(AC=\sqrt{BC^2-AB^2}=12\left(cm\right)\)
Áp dụng HTL: \(\left\{{}\begin{matrix}AH=\dfrac{AB\cdot AC}{BC}=7,2\left(cm\right)\\BH=\dfrac{AB^2}{BC}=5,4\left(cm\right)\end{matrix}\right.\)
Áp dụng PTG: \(HM=\sqrt{AM^2-AH^2}=2,1\left(cm\right)\)
Vậy \(S_{AHM}=\dfrac{1}{2}HM\cdot AH=\dfrac{1}{2}\cdot2,1\cdot7,2=7,56\left(cm^2\right)\)


bài 9
tam giác ABC vuông tại A có
* BC2=AB2+AC2
BC2=152+202=625
BC=25cm
* AH.BC=AB.AC
AH.25=15.20
AH.25=300
AH=12cm
tam giác ABH vuông tại H có
BH2=AB2-AH2
BH2=152-122=81
BH=9cm
tam giác ABC vuông tại A có
*AB2=BH.BC
225=9.BC
BC=25cm
CH=BC-BH=25-9=16cm
*AC2=BC2-AB2
AC2=252-152=400
AC=20cm

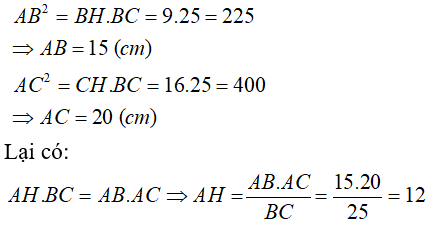
Lời giải:
Áp dụng hệ thức lượng trong tam giác vuông:
$AB^2=BH.BC$
$BH=\frac{AB^2}{BC}=\frac{9^2}{15}=5,4$ (cm)
$CH=BC-BH=15-5,4=9,6$ (cm)
$AC=\sqrt{BC^2-AB^2}=\sqrt{15^2-9^2}=12$ (cm) theo định lý Pitago
$AH=\frac{2S_{ABC}}{BC}=\frac{AB.AC}{BC}=\frac{9.12}{15}=7,2$ (cm)
Hình vẽ: