Gọi x (sản phẩm) là năng suất lúc đầu của công nhân đó (x > 0)

+) Nếu năng suất là x sản phẩm thì thời gian làm là 30/x h

+) Nếu năng suất là x + 5 sản phẩm thì thời gian làm là 30/x h

Vì thời gian chênh lệch nếu vẫn giữ nguyên năng suất và tăng tăng suất là 1 giờ nên ta có phương trình:

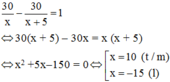
Vậy năng suất lúc đầu của người công nhân đó là 10 sản phẩm

Đáp án: D

Gọi số sản phẩn dự kiến làm mỗi ngày là x>3 sản phẩm và thời gian dự định làm là y>2 ngày

\(\Rightarrow\) Số sản phẩm dự định làm là \(xy\) sản phẩm

Do tăng năng suất mỗi ngày 5 sản phẩm thì thời gian hoàn thành sớm hơn 2 ngày nên:

\(\left(x+5\right)\left(y-2\right)=xy\Rightarrow-2x+5y-10=0\)

Do giảm năng suất 3 sản phẩm mỗi ngày thì thời gian hoàn thành muộn 2 ngày nên:

\(\left(x-3\right)\left(y+2\right)=xy\Rightarrow2x-3y-6=0\)

Ta được hệ: \(\left\{{}\begin{matrix}-2x+5y-10=0\\2x-3y-6=0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x=15\\y=8\end{matrix}\right.\)

Công nhân đó được giao làm: \(15.8=120\) sản phẩm

Con cảm ơn ạ

Gọi số sản phẩm công nhân làm trong 1 h là x( x<45)

Vì thực tế mỗi giờ sản xuất thêm 1 sp nên số sp làm trong 1 h thực tế là: x+1

Vì hoàn thành sớm hơn dự định 18 phút và còn làm thêm được 2 sản phẩm nên ta có pt:

\(\dfrac{45}{x}-\dfrac{47}{x+1}=\dfrac{3}{10}\)

⇔x=9(TM)

Vậy trong 1h người đó làm được 9 sp theo dự định

Bài 21:

Gọi x (sản phẩm/giờ) là năng suất dự kiến ban đầu của người đó \(\left(x\inℕ^∗\right)\)

=> x + 2 (sản phẩm/giờ) là năng suất lúc sau của người đó

Theo bài ta có phương trình sau:

\(\frac{150}{x}-\frac{1}{2}-2=\frac{150-2x}{x+2}\)

\(\Leftrightarrow300\left(x+2\right)-x\left(x+2\right)-4x\left(x+2\right)=2\left(150-2x\right)x\)

\(\Leftrightarrow300x+600-x^2-2x-4x^2-8x=300x-4x^2\)

\(\Leftrightarrow x^2+10x-600=0\)

\(\Leftrightarrow\left(x-20\right)\left(x+30\right)=0\)

\(\Leftrightarrow\orbr{\begin{cases}x-20=0\\x+30=0\end{cases}}\Leftrightarrow\orbr{\begin{cases}x=20\left(tm\right)\\x=-30\left(ktm\right)\end{cases}}\)

Vậy ban đầu năng suất người đó là 20 (sản phẩm/giờ)

Bài 22:

Gọi x (sản phẩm/giờ) là năng suất dự kiến của người đó \(\left(x\inℕ^∗;x< 20\right)\)

=> x + 1 (sản phẩm/giờ) là năng suất lúc sau của người đó 

Theo bài ra ta có phương trình:

\(\frac{80}{x+1}-\frac{1}{5}=\frac{72}{x}\)

\(\Leftrightarrow400x-x\left(x+1\right)=360\left(x+1\right)\)

\(\Leftrightarrow400x-x^2-x=360x+360\)

\(\Leftrightarrow x^2-39x+360=0\)

\(\Leftrightarrow\left(x-15\right)\left(x-24\right)=0\)

\(\Leftrightarrow\orbr{\begin{cases}x-15=0\\x-24=0\end{cases}}\Leftrightarrow\orbr{\begin{cases}x=15\left(tm\right)\\x=24\left(ktm\right)\end{cases}}\)

Vậy năng suất ban đầu là 15 sp/giờ

Gọi số sản phẩm công nhân đó dự định làm trong mỗi giờ là x( x > 0 )

Thời gian công nhân đó dự định làm xong 150 sản phẩm là 150/x (giờ)

2 giờ công nhân đó làm được 2x sản phẩm 

Số sản phẩm còn lại là 150 - 2x sản phẩm

Sau 2 giờ công nhân tăng năng suất được 2 sản phẩm

=> Số sản phẩm công nhân đó làm được trong 1 giờ là x+2 sản phẩm

=> Thời gian công nhân làm hết 150 - 2x sản phẩm còn lại là (150 - 2x)/(x+2)

Theo bài ra ta có phương trình :

\(2+\dfrac{150-2x}{x+2}=\dfrac{150}{x}-\dfrac{1}{2}\)( bạn tự giải tiếp )

=> x₁ = -30 (ktm) ; x₂ = 20 (tm)

Vậy sản phẩm công nhân đó dự định làm trong mỗi giờ là 20 sản phẩm

Gọi năng suất dự định là x (0 < x < 20, sản phẩm/giờ)

Sản phẩm làm được sau 2 giờ là: 2x (sản phẩm)

Số sản phẩm còn lại là 120 – 2x (sản phẩm)

Năng suất sau khi cải tiến là x + 3 (sản phẩm/giờ)

Thời gian làm số sản phẩm còn lại là: 120 - 2 x x + 3  (giờ)

Do sau khi cải tiến người đó hoàn thành kế hoạch sớm hơn dự định 1 giờ 36 phút

Đổi 1 giờ 36 phút bằng 1,6 giờ

Theo bài ra ta có phương trình:

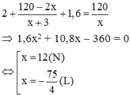
Vậy năng suất dự định của công nhân đó là 12 sản phẩm/giờ

Đáp án C

x: Số SP

=>

Thời gian dự định: x/12

Thời gian thực thế (x/2)/12 + (x/2)/15

\(\frac{x}{12}\)- (\(\frac{x}{2.12}\)+\(\frac{x}{2.15}\)) = 1

=> \(\frac{x}{24}\)- \(\frac{x}{30}\) = 1

=> \(\frac{x}{120}\) = 1

=> x = 120

mk vẫn chưa hiểu...từ chỗ x/12-(x/2.12 +x/2.15)=1