Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
Thời gian người ấy đi hết quãng đường là:
![]()
với ![]() và
và ![]()

Tốc độ trung bình của nười ấy trên cả quãng đường:

![]()

Vì khối lượng ô tô không đổi, lực trong hai trường hợp là như nhau nên gia tốc như nhau. Ta có:
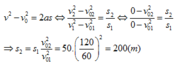
=> Chọn D

Chọn đáp án B
Đổi đơn vị v 0 = 36 k m / h = 10 m / s v = 54 k m / h = 15 m / s (Chú ý: 1 k m / h = 10 3 60.60 m / s = 1 3 , 6 m / s )
v 2 − v 0 2 = 2 a . s ⇒ a = v 2 − v 0 2 2 s = 15 2 − 10 2 2.625 = 0 , 1 m / s 2

Chọn đáp án D
Vận tốc xe khi xuôi gió v = 15 + 1 = 16 k m / h
Thời gian đi xuôi gió t 1 = 28 16 = 1 , 75 h
Vận tốc xe khi ngược gió v = 15 − 1 = 14 k m / h
Thời gian xe đi ngược gió t 2 = 28 14 = 2 h
Thời gian tổng cộng đi và về là t = t 1 + t 2 = 3 , 75 h

Gọi khoảng cách giữa hai bến sông là S = AB, giả sử nước chảy từ A đến B với vận tốc u ( u < 3km/h )
- Thời gian thuyền chuyển động từ A đến B là: t1 = \(\frac{S}{v_1+u}\)
- Thời gian chuyển động của ca nô là: t2 = \(\frac{2S}{v_2-u}+\frac{2S}{v_2+u}\)
Theo bài ra: t1 = t2 \(\Leftrightarrow\frac{S}{v_1+u}=\frac{2S}{v_2-u}+\frac{2S}{v_2+u}\)
Hay: \(\frac{1}{v_1+u}=\frac{2}{v_2-u}+\frac{2}{v_2+u}\Rightarrow\)\(u^2+4v_2u+4v_1v_2-v^2_2=0\) \(\left(1\right)\)
Giải phương trình (1) ta được: \(u\approx\text{ - 0,506 km/h }\)
Vậy nước sông chảy theo hướng BA với vận tốc gần bằng 0,506 km/h
b. Nếu nước chảy nhanh hơn thì thời gian ca nô đi về về B (với quãng đường như câu a) có thay đổi không? vì sao?
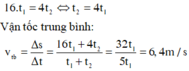
Gọi quãng đường người đi xe đạp là 3S.
Trên 1/3 đoạn đầu: \(v_1=\frac{S}{t_1}\Rightarrow t_1=\frac{S}{v_1}=\frac{S}{14}\)
1/3 quãng đường tiếp theo: \(v_2=\frac{S}{t_2}\Rightarrow t_2=\frac{S}{v_2}=\frac{S}{12}\)
1/3 quãng đường còn lại: \(v_3=\frac{S}{t_3}\Rightarrow t_3=\frac{S}{v_3}=\frac{S}{10}\)
Tổng thời gian đi trên đoạn đường 3S là: \(t_1+t_2+t_3=\frac{S}{14}+\frac{S}{12}+\frac{S}{10}=\frac{107}{420}S\)
Vận tốc TB: \(v_{TB}=\frac{3S}{t_1+t_2+t3}=\frac{3S}{\frac{107}{420}S}=\frac{1260}{107}\approx11,78\)(km/h)
lý 8 à dễ mà