Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: \(M=m^2\left(m+n\right)-n^2m-n^3\)
\(=m^2\left(m+n\right)-n^2\left(m+n\right)\)
\(=\left(m+n\right)^2\left(m-n\right)\)
\(=\left(-2017+2017\right)^2\cdot\left(-2017-2017\right)\)
=0
b: \(N=n^3-3n^2-n\left(3-n\right)\)
\(=n^2\left(n-3\right)+n\left(n-3\right)\)
\(=n\left(n-3\right)\left(n+1\right)\)
\(=13\cdot10\cdot14=1820\)

B1:
[(m+n)+(2m-3n)]^2
= (m+n)^2 + 2(m+n)(2m-3n) + (2m-3n)^2
= m^2 +2mn +n^2 + 4m^2 - 6mn + 4mn - 6n^2 + 4m^2 - 12mn + 9n^2
= 9m^2 - 12mn + 4n^2
B2,3
bn lm theo hdt ( a +b + c) ^2 = a^2 + b^2 + c^2 + 2ab + 2ac + 2bc nha

a: A=3(x^2-y^2)-2(x-y)^2
=3(x+y)(x-y)-2(x-y)^2
=(x-y)(3x+3y-2x+2y)
=(x-y)(x+5y)
=(4+4)(4-5*4)
=8*(-16)=-128
b: \(B=\left(2x-4\right)^2+2\cdot\left(2x-4\right)\left(x+1\right)+\left(x+1\right)^2\)
=(2x-4+x+1)^2
=(3x-3)^2
Khi x=-1/2 thì B=(-3/2-3)^2=(-9/2)^2=81/4
c: \(C=x^2\left(5-4\right)+y^2\left(4-6\right)+z^2\left(6+4\right)\)
=x^2-2y^2+10z^2
=6^2-2*5^2+10*4^2
=146
d: x=9 thì x+1=10
\(D=x^{2017}-x^{2016}\left(x+1\right)+x^{2015}\left(x+1\right)-...-x^2\left(x+1\right)+x\left(x+1\right)-\left(x+1\right)\)
=x^2017-x^2017+x^2016+...-x^3-x^2+x^2+x-x-1
=-1
a: A=3(x^2-y^2)-2(x-y)^2
=3(x+y)(x-y)-2(x-y)^2
=(x-y)(3x+3y-2x+2y)
=(x-y)(x+5y)
=(4+4)(4-5*4)
=8*(-16)=-128

a: \(N=\left(2x-3y\right)\left(2x+3y\right)=\left(2x\right)^2-\left(3y\right)^2\)
\(=4x^2-9y^2\)
Thay x=1/2 và y=1/3 vào N, ta được:
\(N=4\cdot\left(\dfrac{1}{2}\right)^2-9\left(\dfrac{1}{3}\right)^2\)
\(=4\cdot\dfrac{1}{4}-9\cdot\dfrac{1}{9}\)
=1-1
=0
b: \(N=\left(2x-y\right)\left(4x^2+2xy+y^2\right)\)
\(=\left(2x-y\right)\left[\left(2x\right)^2+2x\cdot y+y^2\right]\)
\(=\left(2x\right)^3-y^3=8x^3-y^3\)
Khi x=1 và y=3 thì \(N=8\cdot1^3-3^3=8-27=-19\)

Easy \(x^2-n^2-2xy+y^2-m^2+2mn\)
\(=\left(x^2-2xy+y^2\right)-\left(n^2-2mn+m^2\right)\)
\(=\left(x-y\right)^2-\left(n-m\right)^2\)
\(=\left(x-y-n+m\right)\left(x-y+n-m\right)\)
\(x^2-n^2-2xy+y^2-m^2+2mn\)
\(=\left(x^2-2xy+y^2\right)-\left(n^2-2mn+m^2\right)\)
\(=\left(x-y\right)^2-\left(n-m\right)^2\)
\(=\left(x-y-n+m\right)\left(x-y+n-m\right)\)

Bài 1
1)
a) x²(x - 2y) - 3xy(x - 2y)
= x(x - 2y)(x - 3y)
b) x² + 2xy + y² - 9z²
= (x² + 2xy + y²) - 9z²
= (x + y)² - (3z)²
= (x + y + 3z)(x + y - 3z)
2) 5x(x - 3) - x + 3 = 0
5x(x - 3) - (x - 3) = 0
(x - 3)(5x - 1) = 0
x - 3 = 0 hoặc 5x - 1 = 0
*) x - 3 = 0
x = 0 + 3
x = 3
*) 5x - 1 = 0
5x = 1
x = 1/5
Vậy x = 1/5; x = 3

Bài 1:
a: \(\left(\dfrac{1}{3}x+2\right)\left(3x-6\right)\)
\(=x^2-3x+6x-12\)
\(=x^2+3x-12\)
b: \(\left(x+3\right)\left(x^2-3x+9\right)=x^3+27\)
c: \(\left(-2xy+3\right)\left(xy+1\right)\)
\(=-2x^2y^2-2xy+3xy+3\)
\(=-2x^2y^2+xy+3\)
d: \(x\left(xy-1\right)\left(xy+1\right)\)
\(=x\left(x^2y^2-1\right)\)
\(=x^3y^2-x\)
Bài 2:
a: Ta có: \(M=\left(3x+2\right)\left(9x^2-6x+4\right)\)
\(=27x^3+8\)
\(=27\cdot\dfrac{1}{27}+8=9\)
b: Ta có: \(N=\left(5x-2y\right)\left(25x^2+10xy+4y^2\right)\)
\(=125x^3-8y^3\)
\(=125\cdot\dfrac{1}{125}-8\cdot\dfrac{1}{8}\)
=0
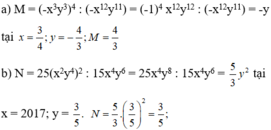


Bài 1:
e: Ta có: \(x\left(y-x\right)^2-x^2+2xy-y^2\)
\(=x\left(x-y\right)^2-\left(x-y\right)^2\)
\(=\left(x-y\right)^2\cdot\left(x-1\right)\)
Bài 2:
a: Ta có: \(M=m^2\left(m+n\right)-n^2m-n^3\)
\(=m^2\left(m+n\right)-n^2\left(m+n\right)\)
\(=\left(m+n\right)^2\cdot\left(m-n\right)\)
\(=\left(-2017+2017\right)^2\cdot\left(-2017-2017\right)\)
=0