Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi số đầu là x.
Cấp số cộng là q.
=> Số đầu, thứ 2. 3,4,5 là x,x+q,x+2q,x+3q,x+4q.
Tổng số 1 và 3 là x + (x+2q) = 28
Tổng số 3 và cuối là (x+2q)+(x+4q)=40.
Ta đã có 2 phương trình tạo thành 1 hệ phương trình.
Giải hệ tìm x và q.
Chúc em học tốt!

2/ \(\left(a+b\right)^k\Rightarrow k+1\left(so-hang\right)\)
\(\Rightarrow n+6+1=17\Rightarrow n=10\)
6/ \(\left(2a-1\right)^6=\sum\limits^6_{k=0}C^k_6.2^{6-k}.\left(-1\right)^k.a^{6-k}\)
\(\Rightarrow tong-3-so-hang-dau=C^0_6.2^6+C^1_6.2^5.\left(-1\right)+C^2_6.2^4.\left(-1\right)^2=...\)
7/ \(\left(x-\sqrt{y}\right)^{16}=\left(x-y^{\dfrac{1}{2}}\right)^{16}\)
\(\Rightarrow tong-2-so-hang-cuoi=C^{16}_{16}+C^{15}_{16}=...\)

Halo lau ko gap :)
\(\left\{{}\begin{matrix}u_1=\sqrt{2}\\u_2=u_1.q=-2\end{matrix}\right.\Rightarrow q=-\dfrac{2}{\sqrt{2}}=-\sqrt{2}\)
\(u_n=64\sqrt{2}=u_1.q^{n-1}\Leftrightarrow\sqrt{2}.\left(-\sqrt{2}\right)^{n-1}=64\sqrt{2}\)
\(\Leftrightarrow\left(-\sqrt{2}\right)^{n-1}=64\Rightarrow n-1=\log_{\sqrt{2}}64=12\Leftrightarrow n=13\)
\(S_{13}=u_1.\dfrac{q^{13}-1}{q-1}=\sqrt{2}.\dfrac{\left(-\sqrt{2}\right)^{13}-1}{-\sqrt{2}-1}=...\)
Check lại số má hộ tui nhó, số ghê quá

Gọi 4 số cần tìm là \(a_1,a_2,a_3,a_4\). Theo đầu bài ta có hệ :
\(\begin{cases}a_2^2=a_1a_3\\2a_3=a_2+a_4\\a_1+a_4=14\\a_2+a_3=12\end{cases}\) \(\Leftrightarrow\begin{cases}2a_1q^2=a_1q+a_2+d\left(1\right)\\a_1+a_2+d=14\left(2\right)\\a_1q+a_1q^2=12\left(3\right)\\a_2+a_2+d=12\left(4\right)\end{cases}\)
\(\Leftrightarrow\begin{cases}a_2^2=a_1\left(a_2+d\right)\left(5\right)\\a_2+2d=14-a_1\\a_1=\frac{12}{q+q^2}\\d=12-2a_2\end{cases}\)
Giải hệ thống các phương trình ta có kết quả \(\left(2,4,8,12\right)\left(\frac{25}{2},\frac{15}{2}\frac{9}{2}\frac{3}{2}\right)\)

Chọn D
Gọi 4 số phải tìm là a1, a2, a3, a4. Theo đầu bài Ta có hệ:
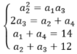
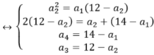
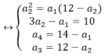
Giải các hệ phương trình Ta có kết quả a1=2, a2=4, a3=8 và a4=12
Chọn D

Chọn B.
Gọi bốn số đó là a ;b ;c ;d ta có hệ:
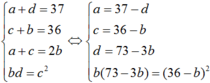
Giải ra ta được : b = 16 ; c = 20 ; d = 25 ; a = 12.

a) Ta có số hạng tổng quát của dãy số \({u_n} = 5n + 1\;\left( {n\; \in {N^*}} \right)\).
b) Các số hạng của dãy số là: 6; 11; 16; 21; 26.
Số hạng đầu của dãy số là: 6 và số hạng cuối của dãy số là 26.
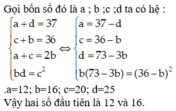
1/ Gọi 4 số đó lần lượt là a;b;c;d
3 số đầu là 3 số hạng liên tiếp của CSN \(\Rightarrow ac=b^2\)
Tương tự: \(b+d=2c\) ; \(a+d=32\) ; \(b+c=24\)
\(\Rightarrow a+b+c+d=a+3c=56\Rightarrow a=56-3c\)
\(b+c=24\Rightarrow b=24-c\)
\(\Rightarrow\left(56-3c\right)c=\left(24-c\right)^2\)
Giải pt bậc 2 này ra c sau đó thế ngược lên tìm nốt a;b;d
2. Gọi số hạng đầu của CSN là \(u_1=3\) ; công bội \(q\) và số số hạng là \(n\)
\(u_n=u_1q^{n-1}\Rightarrow3q^{n-1}=1536\Rightarrow q^{n-1}=512\Rightarrow q^n=512q\)
Lại có:
\(S_n=u_1\frac{q^n-1}{q-1}=2047\Rightarrow\frac{3\left(512q-1\right)}{q-1}=2047\)
\(\Rightarrow1536q-3=2047q-2047\Rightarrow q=4\)
Vậy CSN đó có \(u_1=3;q=4\)