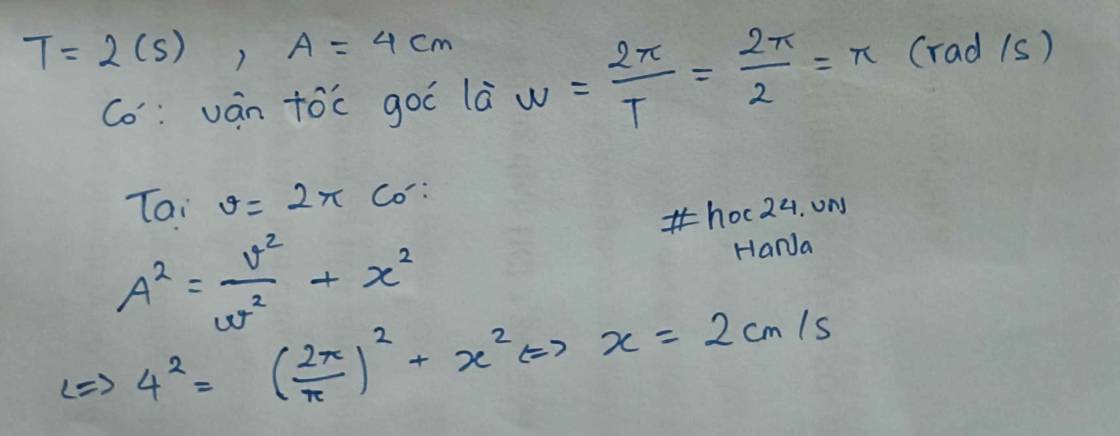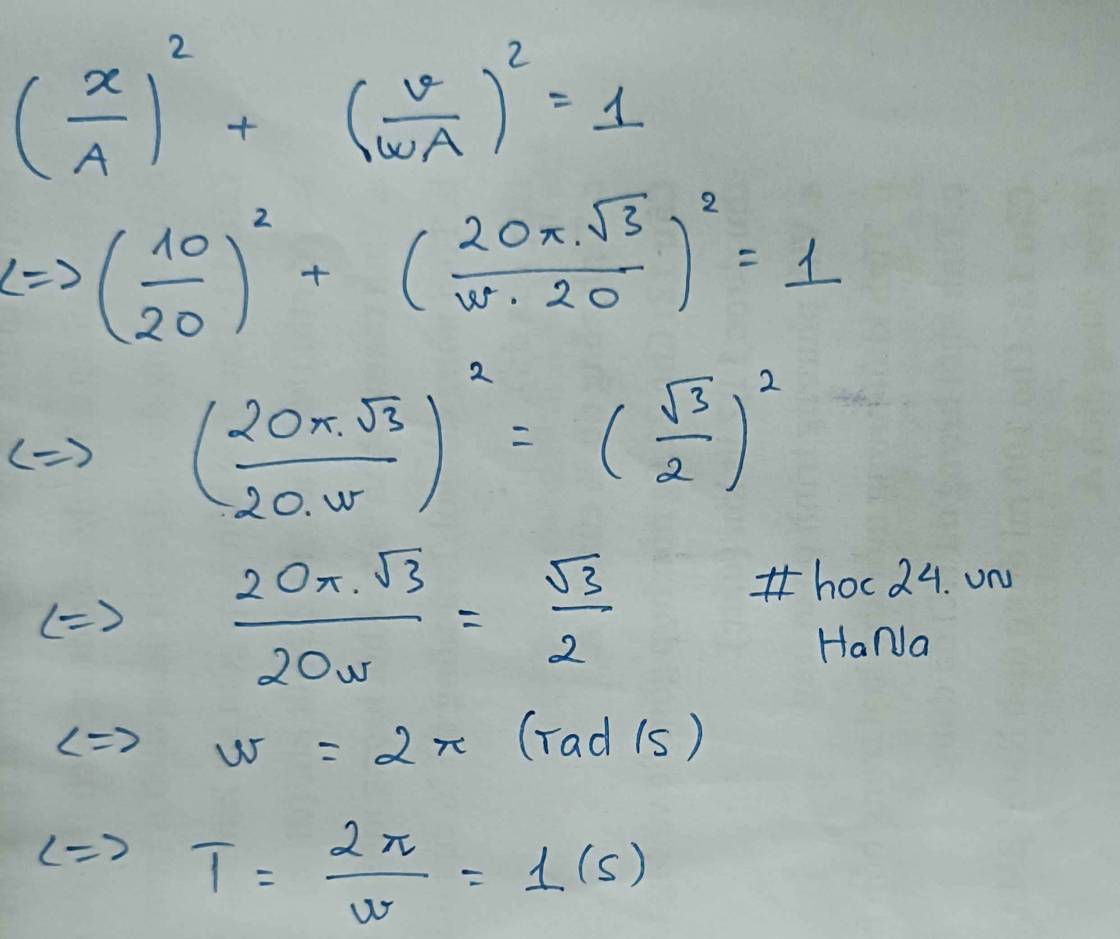Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Vận tốc của vật vào thời điểm đó là: \(v=A\omega=\dfrac{2\pi A}{T}=\dfrac{2\pi\cdot10}{2}=10\pi\left(cm/s\right)\)

Thời gian ngắn nhất để vật đi từ VTCB đến li độ \(x=-\dfrac{A}{2}\) là \(\dfrac{T}{12}\)
\(\Rightarrow\dfrac{T}{12}=0,1\Rightarrow T=1,2\left(s\right)\)

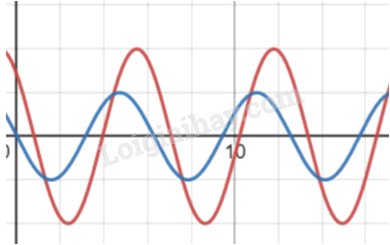
Dao động 1 vẽ với biên độ A và chu kì T
Dao động 2 có cùng chu kì với dao động 1 và biên độ \(A_2=2A\) vị trí đầu tiên của dao động thứ hai bằng \(\dfrac{\sqrt{2}}{2}A_2\) và ở thời điểm \(\dfrac{T}{8}\) thì dao động 2 sẽ đi qua vị trí cân bằng.
Cứ thế tiếp tục vẽ 2 chu kì dao động của hai dao động
Đường màu xanh là dao động thứ nhất, đường màu đỏ là dao động thứ 2

Cái kia lỗi công thức tí, mình làm lại đây nha=)
Phương trình vận tốc của vật trong dao động điều hòa là:
`[ v(t) = -A \omega \sin(\omega t + \varphi) ]`
Phương trình vận tốc của vật là:
`[ v(t) = -4\pi \sin(2\pi t + 0.5)) ]`
$HaNa$

Có: \(f=\dfrac{w}{2\pi}=10\Rightarrow w=20\pi\)
Phương trình dao động của vật là:
\(x=4cos\left(20\pi t-\dfrac{\pi}{2}\right)\)