Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

ta có \(v^2-v_0^2=2aS\)
\(\Leftrightarrow v^2-v_0^2=-2\mu g.S\Rightarrow S=\dfrac{v_0^2}{2\mu g}\)
\(A_{Fms}=F.S.\cos\left(180^0\right)=\mu N.\dfrac{v_0^2}{2\mu g}\cos\left(180^0\right)\) Mà N=P=mg
Thay N=P=mg vào ta được: \(A_{Fms}=\mu mg\dfrac{v_0^2}{2\mu g}\cos\left(180^0\right)=-45\left(J\right)\)

Đáp án B
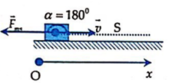
Lực ma sát tác dụng lên vật có độ lớn bằng công thức: F = μ m g
Quãng đường vật trượt đến khi dừng là:
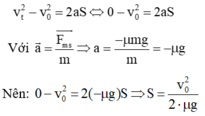
Công của lực ma sát đã thực hiện đến khi vật dừng lại là
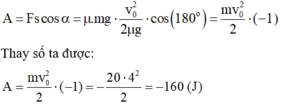
Do A < 0 và lực có tác dụng cản trở lại chuyển động, khi đó A gọi là công cản.

Đáp án B
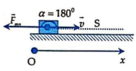
Lực ma sát tác dụng lên vật có độ lớn bằng công thức: F = μmg
Quãng đường vật trượt đến khi dừng là:
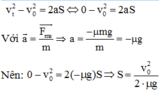
Công của lực ma sát đã thực hiện đến khi vật dừng lại là
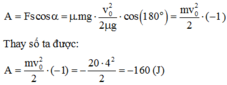
Do A < 0 và lực có tác dụng cản trở lại chuyển động, khi đó A gọi là công cản.

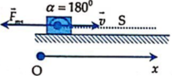
Lực ma sát tác dụng lên vật có độ lớn bằng công thức:
![]()
Quãng đường vật trượt đến khi dừng là:
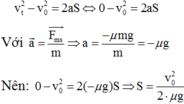
Công của lực ma sát đã thực hiện đến khi vật dừng lại là
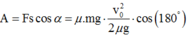
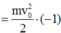
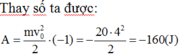
Do A < 0 và lực có tác dụng cản trở lại chuyển động, khi đó A gọi là công cản.
Đáp án B

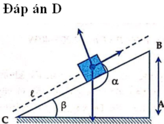
Công của trọng lực thực hiện từ lúc vật lên dốc đến lúc dừng lại trên dốc bằng: Ap=mgh
Với h là hiệu độ cao từ vị trí đầu đến vị trí cuối, tính theo hình ta có:
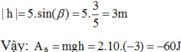

Chọn đáp án B
Áp dụng công thức
![]()
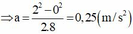
Khi có lực ma sát ta có
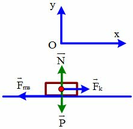
Chọn hệ quy chiếu Oxy như hình vẽ , chiều dương (+) Ox là chiều chuyển động
Áp dụng định luật II Newton ![]()
Chiếu lên trục Ox: ![]()
Chiếu lên trục Oy:
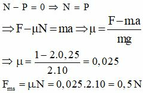
B
Tính a
tính vận tốc áp dụng công thức liên hệ '
my = F*a / m*g

Lực ma sát tác dụng lên vật có độ lớn bằng công thức:
Quãng đường vật trượt đến khi dừng là:
Công của lực ma sát đã thực hiện đến khi vật dừng lại là
Ta có : \(F_{ms}=N.\mu=mg\mu=100u\left(N\right)\)
Lại có : \(v^2-v^2_0=2as\)
\(\Rightarrow2as=0^2-3^2=-9\)
\(\Rightarrow S=-\dfrac{9}{2a}\)
Mà \(F_{ms}=ma\)
\(\Rightarrow a=\dfrac{-F}{m}=\dfrac{-100u}{10}=-10u\left(\dfrac{m}{s^2}\right)\) ( \(\overrightarrow{a}\uparrow\downarrow\overrightarrow{F}\) )
\(\Rightarrow S=-\dfrac{9}{-2.10u}=\dfrac{9}{20u}\left(m\right)\)
Ta có : \(A=F_{ms}.s.cos180=\dfrac{\left(-1\right).9}{20u}.100u=-45\left(J\right)\)
Vậy ...
