Bạn tham khảo cách làm tương tự tại đây nhé:

Câu hỏi của Anh Aries - Toán lớp 8 - Học toán với OnlineMath

Mình cũng làm theo ban quản lý tham khảo tại link này:

https://olm.vn/hoi-dap/detail/7093348726.html

~Hok tốt~

Gọi chiều dài quãng đường AB là \(x\left( {km} \right)\). Điều kiện \(x > 0\).

Vì ban đầu xe dự định đi với vận tốc 50 \(km/h\) trên suốt quãng đường nên thời gian dự định đi hết quãng đường AB là \(\frac{x}{{50}}\) (giờ).

\(\frac{2}{3}\) quãng đường đầu tiên là \(\frac{2}{3}x\) đi với vận tốc 50 \(km/h\) nên thời gian đi hết \(\frac{2}{3}\) quãng đường đầu tiên là \(\frac{2}{3}x:50 = \frac{2}{{150}}x\) (giờ).

\(\frac{1}{3}\) quãng đường đầu tiên là \(\frac{1}{3}x\) đi với vận tốc 40 \(km/h\) nên thời gian đi hết \(\frac{1}{3}\) quãng đường sau là \(\frac{1}{3}x:40 = \frac{1}{{120}}x\) (giờ).

Tổng thời gian đi thực tế là \(\frac{2}{{150}}x + \frac{1}{{120}}x\) (giờ)

Đổi 30 phút = \(\frac{1}{2}\) giờ

Vì ô tô đến B chậm hơn dự định \(\frac{1}{2}\) giờ nên ta có phương trình:

\(\frac{2}{{150}}x + \frac{1}{{120}}x - \frac{x}{{50}} = \frac{1}{2}\)

\(\frac{{2.4}}{{150.4}}x + \frac{{1.5}}{{120.5}}x - \frac{{x.12}}{{50.12}} = \frac{{1.300}}{{2.300}}\)

\(\frac{{8x}}{{150.4}} + \frac{{5x}}{{120.5}} - \frac{{12x}}{{50.12}} = \frac{{300}}{{600}}\)

\(8x + 5x - 12x = 300\)

\(x = 300\) (thỏa mãn điều kiện)

Vậy độ dài quãng đường AB là 300 \(km\).

Đổi 24p=\(\dfrac{2}{5}h\)

Gọi quãng đường AB là x(km)

Thời gian đi nửa quãng đường là: \(\dfrac{x}{2}:60\)=\(\dfrac{x}{120}\) (h)

Thời gian đi nửa quãng đường sau là: \(\dfrac{x}{2}:50=\dfrac{x}{100}\) (h)

Thời gian đến B theo dự định là : \(\dfrac{x}{60}\) (h)

Vì xe máy đến B muộn 24 phút nên ta có PT:

\(\dfrac{x}{120}+\dfrac{x}{100}=\dfrac{x}{60}+\dfrac{2}{5}\)

Giả PT trên ta được x =240

Vậy quãng đường AB dài 240 km

-Gọi quãng đường AB là x (km) (x>0)

-Đổi 15 phút=\(\dfrac{1}{4}\)h ; 10 phút=\(\dfrac{1}{6}\)h

-Quãng đường người đó đi được trong 15 phút đầu: \(40.\dfrac{1}{4}=10\left(km\right)\)

                  Quãng đường còn lại (km)  Vận tốc (km/h) Thời gian (h)

Dự định                    x-10                               40                 \(\dfrac{x-10}{40}\)

Thực tế                     x-10                              36                   \(\dfrac{x-10}{36}\)

-Quãng đường còn lại xe đi được là: x-10 (km)

-Thời gian xe đi hết quãng đường còn lại dự định: \(\dfrac{x-10}{40}\)(h)

-Thời gian xe đi hết quãng đường còn lại dự thực tế: \(\dfrac{x-10}{36}\)(h)

-Vì xe tải đến B chậm hơn 10 phút so với dự định nên ta có phương trình sau:

\(\dfrac{x-10}{36}-\dfrac{x-10}{40}=\dfrac{1}{6}\)

\(\Leftrightarrow\left(x-10\right)\left(\dfrac{1}{36}-\dfrac{1}{40}\right)=\dfrac{1}{6}\)

\(\Leftrightarrow\left(x-10\right).\dfrac{1}{360}=\dfrac{1}{6}\)

\(\Leftrightarrow x-10=60\)

\(\Leftrightarrow x=70\left(km\right)\left(nhận\right)\)

-Vậy quãng đường AB dài 70 km.

Gọi vận tốc ban đầu của người đó là x (km/h; \(x>5\))

Thời gian dự định là \(\dfrac{60}{x}\) (giờ)

Vận tốc lúc sau là x - 5 (km/h)

Thời gian người đó đi trên nửa quãng đường đầu là \(\dfrac{30}{x}\) (giờ)

Thời gian người đó đi trên nửa quãng đường sau là \(\dfrac{30}{x-5}\) (giờ)

Do người đó đến B chậm hơn dự định 1 giờ => ta có phương trình:

\(\dfrac{30}{x}+\dfrac{30}{x-5}=\dfrac{60}{x}+1\)

<=> \(\dfrac{30}{x-5}-\dfrac{30}{x}-1=0\)

<=> \(\dfrac{30x-30\left(x-5\right)-x\left(x-5\right)}{x\left(x-5\right)}=0\)

<=> 30x - 30x + 150 - x² + 5x = 0

<=> x² -5x - 150 = 0

<=> (x-15)(x+10) = 0

Mà x > 5

<=> x - 15 = 0

<=> x = 15 (tm)

KL Vận tốc dự định của người đó là 15 km/h 

Vì thời gian thực tế đi chậm hơn thời gian dự định là 18 phút nên ta có phương trình:

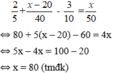
Vậy chiều dài quãng đường AB là 80km.