Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn : C.9
Giải thích:
8n+1111...1 (n thừa số 1 )
\(\Rightarrow\) Tổng số số hạng của 1111...1 là n
\(\Rightarrow\) 8n+n=9n
Mà 9n \(⋮\) 9
\(\Rightarrow\)8n + 1111...1 ( n thừa số 1) \(⋮\) 9

CÂU 1 : 0,0135135135135135
CÂU 2 : 22
CÂU 3 : 1247
CÂU 4 : 2223333444444444
CÂU TRẢ LỜI NÈ

1+11=12
1111+11111=12222
89309+8=89316
93651:1=93551
83626+1=83627
1865+1=1866
87366+8=87374
8276+2=8278
8365-87=8278
1+11=12
1111+11111=12222
89309+8=89317
93651:1=93651
83626+1=83627
1865+1=1866
87366+8=87374
8276+2=8278
8365-87=8278
#Học tốt

1/ Lần ăn kem miễn phí thứ nhất, Khánh sẽ đem 2 que của mình đổi lấy 1 chiếc kem và sau khi ăn hết kem, Khánh lấy lại được 1 que kem. Từ đó số que kem còn lại sau lần thứ nhất Khánh ăn kem miễn phí sẽ là \(20-2+1=19\) (que)
Tương tự như vậy, sau lần ăn kem free thứ hai, Khánh sẽ còn \(19-2+1=18\)(que)
Sau lần ăn kem free thứ ba, Khánh còn \(18-2+1=17\)(que)
[...]
Sau lần ăn kem free thứ 19, Khánh còn 1 que, và 1 que thì không đổi được kem free nữa.
Vậy Khánh có 19 lần được ăn kem free.
2/ Trong nhà thờ có 5 cây nến vì đề bài đã cho.
3/ Câu này em chưa biết.
4/ Câu này có các cách giải thích:
- Chúng ta có thể trừ đi 1 từ số 1111 vô hạn lần vì theo tính chất của số nguyên thì không có số nguyên nhỏ nhất.
- Số 1111 có 4 chữ số 1 nên ta chỉ có thể trừ đi 1 từ số này 4 lần.

ĐKXĐ: \(x\in\left[0;2018\right]\)
\(y'=\dfrac{1009-x}{\sqrt{2018x-x^2}}=0\Rightarrow x=1009\)
Hàm đồng biến trên \(\left(0;1009\right)\)

Gọi tọa độ các giao điểm là \(A\left(a;0;0\right)\); \(B\left(0;b;0\right)\); \(C\left(0;0;c\right)\)
Không làm mất tính tổng quát, chỉ cần xét trường hợp \(a;b;c>0\)
Phương trình mặt phẳng (P) theo đoạn chắn: \(\frac{x}{a}+\frac{y}{b}+\frac{z}{c}=1\)
Ta có: \(S=OA+OB+OC=a+b+c\)
Do \(\left(P\right)\) qua M nên: \(\frac{4}{a}+\frac{1}{b}+\frac{9}{c}=1\)
Áp dụng BĐT Cauchy-Scwarz: \(\frac{2^2}{a}+\frac{1^2}{b}+\frac{3^2}{c}\ge\frac{\left(2+1+3\right)^2}{a+b+c}=\frac{36}{a+b+c}\)
\(\Rightarrow\frac{36}{a+b+c}\le1\Rightarrow a+b+c\ge36\)
\(\Rightarrow S_{min}=36\) khi \(\left\{{}\begin{matrix}a+b+c=36\\\frac{2}{a}=\frac{1}{b}=\frac{3}{c}\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}a=12\\b=6\\c=18\end{matrix}\right.\)
Phương trình (P) khi đó có dạng: \(\frac{x}{12}+\frac{y}{6}+\frac{z}{18}=1\)
Hay chuyển dạng chính tắc: \(3x+6y+2z-36=0\)
Không thấy điểm I ở đâu để tính tiếp cả, nhưng đến đây thì mọi chuyện đơn giản, chỉ cần áp dụng công thức khoảng cách vào là xong.

Chọn C
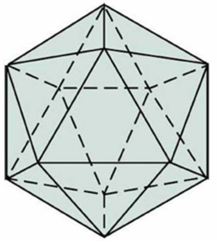
Khối hai mươi mặt đều có các mặt là tam giác nên thuộc loại 3 ; 5 .




sẽ bằng 0 bạn nhé
= 0:))