
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a, - Thấy : \(\widehat{A}+\widehat{B}=180^o\)
Mà 2 góc A và B ở vị trí trong cùng phía .
=> a // b .
b, Ta có : \(\widehat{D}+\widehat{C}=180^o\) ( a//b )
Mà \(\widehat{D}=120^o\)
\(\Rightarrow\widehat{C}=180-120=60^o\)
Vậy ...

a: góc B=180-40-70=70 độ
b: Xét ΔDBC có DB=DC
nên ΔDBC cân tại D
=>góc BDC=180 độ-2*góc C=180-2*40=100 độ

\(a,Ax//By\Rightarrow\widehat{ABy}=\widehat{BAx}=120^0\left(so.le.trong\right)\\ b,\widehat{ABy}=\widehat{BCz}\left(=120^0\right)\)
Mà 2 góc này ở vị trí đồng vị nên \(By//Cz\)
Mà \(By//Ax\) nên \(Cz//Ax\)
Vậy có 3 cặp tia song song là \(Ax//By;By//Cz;Cz//Ax\)

a) Xét tam giác ABC. Ta có:
Vì AD là tia phân giác của góc A nên:
\(\widehat{BAD}=\widehat{DAC}=\frac{\widehat{A}}{2}=40^{^o}\)
\(\widehat{ADB}=180^o-70^o-40^o=70^o\)
Vì \(\widehat{ADB}=\widehat{ABD}=70^o\)nên ABD là tam giác cân.
b)Vì \(\widehat{ADB}\)kề bù với \(\widehat{ADC}\)nên \(\widehat{ADC}=180^o-70^o=110^o\)
Do tam giác ACD là tam giác nên \(\widehat{ACD}=180^o-40^o-110^o=30^o\)
c) Đặt đỉnh ngoài của B là B1.
Ta có: \(\widehat{B_1}=180^o-70^o=110^o\)
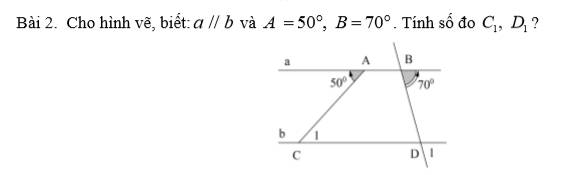
a) Ta có: \(a\perp AB\)
\(b\perp AB\)
=> a//b( từ vuông góc đến song song)
b) Ta có: a//b(cmt)
\(\Rightarrow\widehat{C}=180^0-\widehat{D}=180^0-120^0=60^0\)(2 góc trong cung phía)
a, a//b vì góc A = góc B = 90o (2 góc đồng vị bằng nhau) (*xl nha, mik ko biết viết dấu góc kiểu j :(
b, a // b ➩ góc D + góc C = 180o
Thay số: 120o + góc C = 180o
⇒ góc C = 180o - 120o = 60o