Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

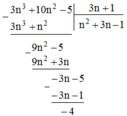
Ta có: 3 n 3 + 10 n 2 - 5 = 3 n + 1 n 2 + 3 n - 1 - 4
Để phép chia đó là chia hết thì 4 ⋮ 3n + 1⇒ 3n + 1 ∈ Ư(4)
3n + 1 ∈ {-4; -2; -1; 1; 2; 4}
3n + 1 = -4⇒ 3n = -5⇒ n = 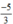 ∉ Z : loại
∉ Z : loại
3n + 1 = -2⇒ 3n = -3⇒ n = -1 ∈ Z
3n + 1 = -1⇒ 3n = -2⇒ n = 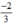 ∉ Z : loại
∉ Z : loại
3n + 1 = 1⇒ 3n = 0⇒ n = 0 ∈ Z
3n + 1 = 2⇒ 3n = 2⇒ n = 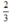 ∉ Z : loại
∉ Z : loại
3n + 1 = 4⇒ 3n = 3⇒ n = 1 ∈ Z
Vậy n ∈ {-1; 0; 1} thì 3 n 3 + 10 n 2 - 5 chia hết cho 3n + 1.

b: \(\Leftrightarrow3n^3+n^2+9n^2+3n-3n-1-4⋮3n+1\)
\(\Leftrightarrow3n+1\in\left\{1;-1;2;-2;4;-4\right\}\)
\(\Leftrightarrow n\in\left\{0;-1;1\right\}\)

a: =>\(n+2\in\left\{1;-1;7;-7\right\}\)
=>\(n\in\left\{-1;-3;5;-9\right\}\)
b: =>n-3+4 chia hết cho n-3
=>\(n-3\in\left\{1;-1;2;-2;4;-4\right\}\)
=>\(n\in\left\{4;2;5;1;7;-1\right\}\)
c: =>3n^3+n^2+9n^2-1-4 chia hết cho 3n+1
=>\(3n+1\in\left\{1;-1;2;-2;4;-4\right\}\)
=>\(n\in\left\{0;-\dfrac{2}{3};\dfrac{1}{3};-1;1;-\dfrac{5}{3}\right\}\)
d: =>10n^2-10n+11n-11+1 chia hết cho n-1
=>\(n-1\in\left\{1;-1\right\}\)
=>\(n\in\left\{2;0\right\}\)

a) Cho 3n +1=0 => n=\(\frac{-1}{3}\)
Sau đó thay vào biểu thức 3n3+10n2-5 sẽ tìm ra n=-4
b) Cho n-1=0 => n=1
Sau đó thay vào biểu thức 10n2+n -10 sẽ tìm ra n=1
Cho mình nha!!! <3

Ta có : n3 - 2n + 3n + 3
= n3 - n + 3
= n(n2 - 1)
= n(n - 1)(n + 1) + 3
Để n3 - 2n + 3n + 3 chia hết cho n - 1
=> n(n - 1)(n + 1) + 3 chia hết cho n - 1
=> 3 chia hết cho n - 1
=> n - 1 thuộc Ư(3) = {-3;-1;1;3}
=> n = {-2;0;2;4}

Lấy 3n^3 + 10n^2 - 5 : 3n + 1 như bình thường, cuối cùng được dư bao nhiêu thì số đó phải chia hết cho 3n + 1. Thì 3n + 1 phải thuộc tập hợp ước của số đó. Và cứ thế tìm n thôi.
a) Ta có: 3n3 + 10n2 - 5 = 3n3 + n2 + 9n2 + 3n - 3n - 1 - 4 =
(3n + 1)(n2 + 3n - 1) - 4
Vì (3n + 1)(n2 + 3n - 1) \(⋮3n+1\left(\forall n\in Z\right)\)
\(\Rightarrow-4⋮3n+1\)
\(\Rightarrow3n+1\inƯ\left(-4\right)\)
\(\Rightarrow3n+1\in\left\{\pm1;\pm2;\pm4\right\}\)
\(\Rightarrow n\in\left\{0;\pm1\right\}\)
b) Ta có: 10n2 + n - 10 = 10n2 - 10n + 9n - 9 - 1 =
(n - 1)(10n + 9) - 1
Vì (n - 1)(10n + 9) \(⋮n-1\left(\forall n\in Z\right)\)
\(\Rightarrow-1⋮n-1\)
\(\Rightarrow n-1\inƯ\left(-1\right)\)
\(\Rightarrow n-1\in\left\{\pm1\right\}\)
\(\Rightarrow n\in\left\{0;2\right\}\)