Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Áp suất trong bánh xe khi bơm xong: p = p0 + p’
Với p’ = 350/0,005= 0,7. 10 5 Pa; p = 1,7.105 Pa lớn hơn 1,5 p 0 nên thể tích sau khi bơm là 2000 c m 3
Mỗi lần bơm có 8.25 = 200 c m 3 không khí ở áp suất p 0 được đưa vào bánh xe. Sau n lần bơm có 200n c m 3 không khí được đưa vào bánh. Ban đầu có 1500 c m 3 không khí ở áp suất p 0 trong bánh xe. Như vậy có thể coi:
Trạng thái 1: p 1 = p 0 ; V 1 = (1500 + 200n)
Trạng thái 2: p 2 = 1,7. 10 5 Pa ; V 2 = 2000 c m 3
Áp dụng định luật Bôi-lơ – Ma-ri-ốt, dễ dàng tìm được n = 19/2 ≈ 10 lần.

Chọn C.
Áp suất trong bánh xe khi bơm xong: p = p0 + p’
Với p’ = F/S = 350/0,005 = 0,7.105 Pa;
→ p = 1,7.105 Pa lớn hơn 1,5p0 nên thể tích sau khi bơm là 2000 cm3.
Mỗi lần bơm có 8.25 = 200 cm3 không khí ở áp suất p0 được đưa vào bánh xe. Sau n lần bơm có 200n cm3 không khí được đưa vào bánh. Ban đầu có 1500 cm3 không khí ở áp suất p0 trong bánh xe. Như vậy có thể coi:
Trạng thái 1: p1 = p0; V1 = (1500 + 200n)
Trạng thái 2: p2 = 1,7.105 Pa; V2 = 2000 cm3
Áp dụng định luật Bôi-lơ – Ma-ri-ốt, dễ dàng tìm được n = 19/2 ≈ 10 lần

Chọn C.
Áp suất trong bánh xe khi bơm xong: p = p 0 + p’
Với p’ = F/S = 350/0,005 = 0,7. 10 5 Pa;
→ p = 1,7. 10 5 Pa lớn hơn 1,5 p 0 nên thể tích sau khi bơm là 2000 c m 3 .
Mỗi lần bơm có 8.25 = 200 c m 3 không khí ở áp suất p 0 được đưa vào bánh xe. Sau n lần bơm có 200n c m 3 không khí được đưa vào bánh. Ban đầu có 1500 c m 3 không khí ở áp suất p 0 trong bánh xe. Như vậy có thể coi:
Trạng thái 1: p 1 = p 0 ; V1 = (1500 + 200n)
Trạng thái 2: p 2 = 1,7. 10 5 Pa; V2 = 2000 c m 3
Áp dụng định luật Bôi-lơ – Ma-ri-ốt, dễ dàng tìm được n = 19/2 ≈ 10 lần

Chọn C.
Áp suất trong bánh xe khi bơm xong: p = p 0 + p’
Với p’ = F/S = 350/0,005 = 0,7. 10 5 Pa;
→ p = 1,7. 10 5 Pa lớn hơn 1,5 p 0 nên thể tích sau khi bơm là 2000 c m 3 .
Mỗi lần bơm có 8.25 = 200 c m 3 không khí ở áp suất p 0 được đưa vào bánh xe. Sau n lần bơm có 200n cm3 không khí được đưa vào bánh. Ban đầu có 1500 cm3 không khí ở áp suất p 0 trong bánh xe. Như vậy có thể coi:
Trạng thái 1: p 1 = p 0 ; V 1 = (1500 + 200n)
Trạng thái 2: p 2 = 1,7. 10 5 Pa; V 2 = 2000 cm3
Áp dụng định luật Bôi-lơ – Ma-ri-ốt, dễ dàng tìm được n = 19/2 ≈ 10 lần

Đáp án: C
Ta có: p = 5.pa = pa + ρ.g.h → h = 4.pa/(ρ.g) = 40m

Gọi F là trọng lượng của xe, V 0 là thế tích mỗi lần bơm, V thể tích săm xe
Ta có trong lần bơm đầu tiên:


Tóm tắt:
\(h=12m\)
\(D=1000kg/m^3\)
\(\Rightarrow d=D.g=1000.10=10000N/m^3\)
\(S=2m^2\)
\(g=10m/s^2\)
========
\(F=?N\)
Áp suất tác dụng lên thợ lặn:
\(p=d.h=10000.12=120000Pa\)
Áp lực tác dụng lên cơ thể người thợ lặn:
\(p=\dfrac{F}{S}\Rightarrow F=p.S=120000.2=240000N\)
⇒ Chọn A

Áp suất trong bánh xe khi bơm xong: p = p0 + p’
Với p’ = 350/0,005= 0,7. 10 5 Pa; p = 1,7.105 Pa lớn hơn 1,5 p 0 nên thể tích sau khi bơm là 2000 c m 3
n’ = 2n = 19 lần.

Đáp án D
- Gọi n là số lần bơm để đưa không khí vào ruột xe.
Vậy thể tích không khí cần đưa vào ruột xe là V1 = nV0 = 80tn cm3.
Và áp suất p1 = l atm.
Áp suất p2 sau khi bơm là
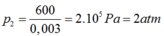
và thể tích V2 = 2000 cm3
Vì quá trình bơm là đẳng nhiệt nên: p1V1 = p2.V2 ó 80n = 2000.2 => n = 50
Vậy số lần cần bơm là 50 lần.
\(a,p_1=\dfrac{F_1}{s_1}=\dfrac{m_1.g}{s_1}=\dfrac{2600.10}{1,3}=20000\left(Pa\right)\\ b,p_2=\dfrac{F_2}{s_2}=\dfrac{m_2.g}{s_2}=\dfrac{45.10}{200.10^{-4}}=22500\left(Pa\right)Vì:20000\left(Pa\right)< 22500\left(Pa\right)\Rightarrow p_1< p_2\)