
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


2: \(A=x^2-10x+25-34=\left(x-5\right)^2-34\ge-34\forall x\)
Dấu '=' xảu ra khi x=5
\(1,C=x^2+x-3\\ \Rightarrow C=\left(x^2+x+\dfrac{1}{4}\right)-\dfrac{13}{4}\\ \Rightarrow C=\left(x+\dfrac{1}{2}\right)^2-\dfrac{13}{4}\ge-\dfrac{13}{4}\)
dấu "=" xảy ra \(\Leftrightarrow x=-\dfrac{1}{2}\)
Vậy \(C_{min}=-\dfrac{13}{4}\Leftrightarrow x=-\dfrac{1}{2}\)
\(2,A=x^2-10x-9\\ \Rightarrow A=\left(x^2-10x+25\right)-34\\ \Rightarrow A=\left(x-5\right)^2-34\)
dấu "=" xảy ra \(\Leftrightarrow x=5\)
Vậy \(A_{min}=-34\Leftrightarrow x=5\)

Bài 8:
a) Ta có: \(A=\left(x-y\right)^3+3xy\left(x-y\right)\)
\(=\left(x-y\right)\left(x^2-2xy+y^2+3xy\right)\)
\(=\left(x-y\right)\left(x^2+xy+y^2\right)\)
\(=x^3-y^3\)
b) Ta có: \(B=\left(x+y\right)^3+3\left(x-y\right)\left(x+y\right)^2+3\left(x-y\right)^2\left(x+y\right)+\left(x-y\right)^3\)
\(=\left(x+y+x-y\right)^3\)
\(=\left(2x\right)^3=8x^3\)

3: Ta có: \(\left(x+3\right)\left(x^2-3x+9\right)-x\left(x-1\right)\left(x+1\right)=27\)
\(\Leftrightarrow x^3-27-x^3+x=27\)
hay x=54

c: \(C=\left(x+y\right)^2-\left(x-y\right)^2\)
\(=\left(x+y+x-y\right)\left(x+y-x+y\right)\)
=4xy
d: \(D=\left(\dfrac{x}{2}-y\right)\left(\dfrac{x}{2}+y\right)=\dfrac{1}{4}x^2-y^2\)

 Mọi người cứu em, tối nay phải nộp rồi.
Mọi người cứu em, tối nay phải nộp rồi.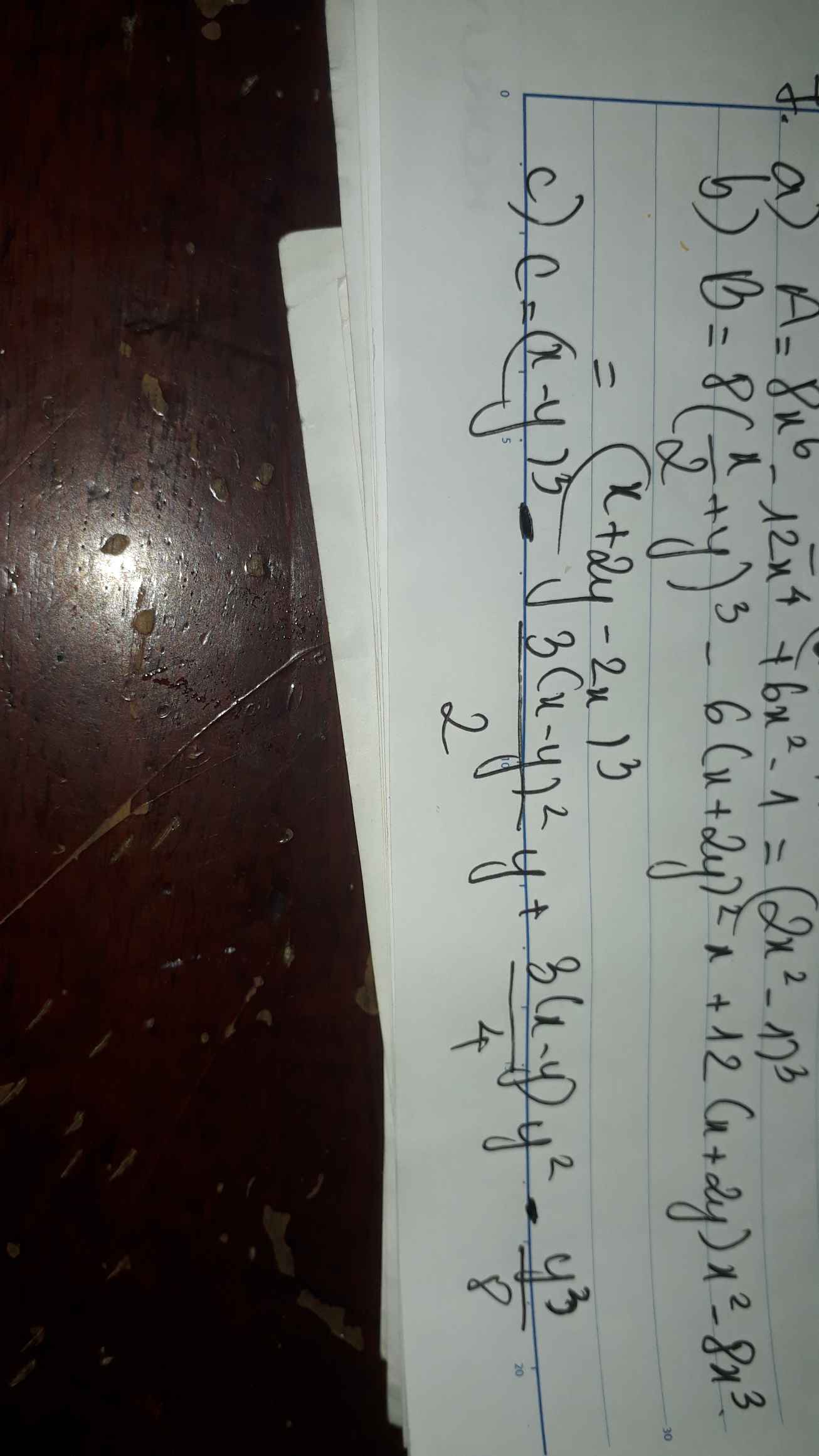

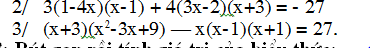
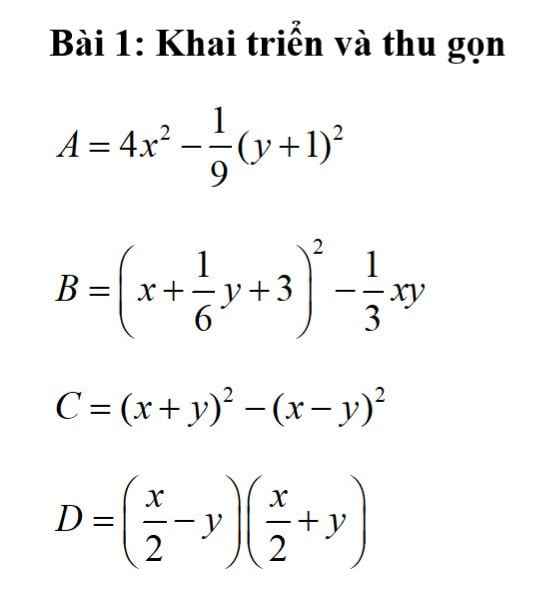
- Ta có:
\(f\left(x\right)=\left(x+1\right)\left(x+2\right)\left(x+3\right)\left(x+4\right)+1\)
\(=\left(x+1\right)\left(x+4\right)\left(x+2\right)\left(x+3\right)+1\)
\(=\left(x^2+5x+4\right)\left(x^2+5x+6\right)+1\)
Đặt: \(\left(x^2+5x+5\right)=a\) ta được:
\(=\left(a-1\right)\left(a+1\right)+1\)
\(=a^2-1+1=a^2\)
Thay lại \(a=\left(x^2+5x+5\right)\) được:
\(\left(x^2+5x+5\right)^2\)
- Đối chiếu với \(\left(ax^2+bx+c\right)^2\)
Vậy \(a=1;b=5;c=5\)