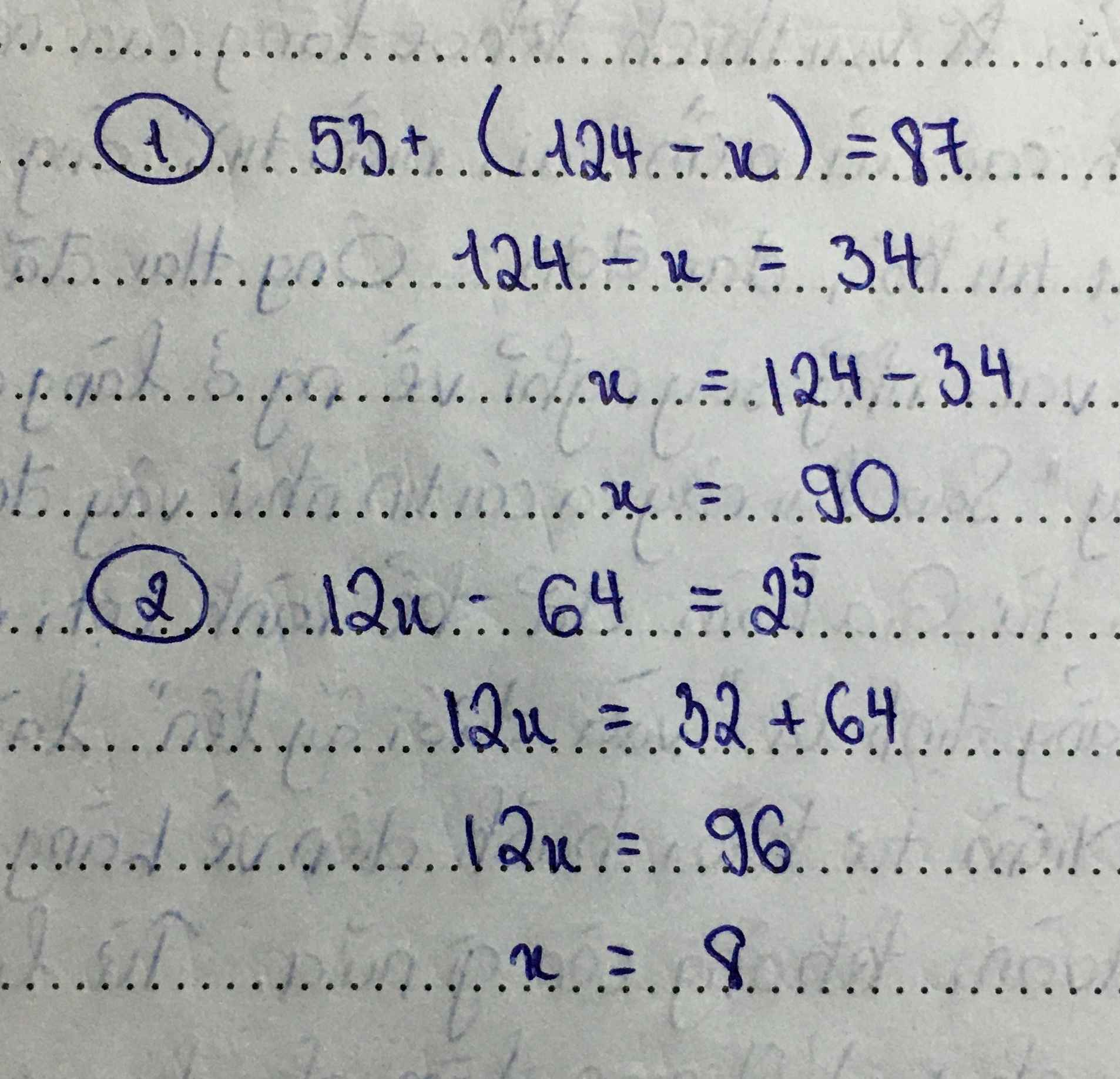\(1,\Rightarrow4^{x+1}=4^{3x}\\ \Rightarrow x+1=3x\\ \Rightarrow2x=1\\ \Rightarrow x=\dfrac{1}{2}\\ 2,\Rightarrow5x-2x=10+10x\\ \Rightarrow7x=-10\\ \Rightarrow x=-\dfrac{10}{7}\)

1. 4^{x + 1} = 64^x

<=> 4^{x + 1} = 4^3x

<=> x + 1 = 3x

<=> 1 = 2x

<=> \(x=\dfrac{1}{2}\)

2. \(\dfrac{x}{2}-\dfrac{x}{5}=1+x\)

<=> \(\dfrac{5x}{10}-\dfrac{2x}{10}=\dfrac{10}{10}+\dfrac{10x}{10}\)

<=> 5x - 2x = 10 + 10x

<=> 5x - 2x - 10x = 10

<=> -7x = 10

<=> \(x=\dfrac{-10}{7}\)

`a,`\(2^x -15= 2^4+1\)

`-> 2^x-15=17`

`-> 2^x=17+15`

`-> 2^x=32`

`-> 2^x=2^5`

`-> x=5`

`b,` Có phải đề là \(\dfrac{x+1}{65}+\dfrac{x+2}{64}=\dfrac{x+3}{63}+\dfrac{x+4}{62}\) ?

`=>`\(\dfrac{x+1}{65}+1+\dfrac{x+2}{64}+1=\dfrac{x+3}{63}+1+\dfrac{x+4}{62}+1\)

`=>`\(\dfrac{x+1+65}{65}+\dfrac{x+2+64}{64}-\dfrac{x+3+63}{63}-\dfrac{x+4+62}{62}=0\)

`=>`\(\dfrac{x+66}{65}+\dfrac{x+66}{64}-\dfrac{x+66}{63}-\dfrac{x+66}{62}=0\)

`=>`\(\left(x+66\right)\left(\dfrac{1}{65}+\dfrac{1}{64}-\dfrac{1}{63}-\dfrac{1}{62}\right)=0\)

Mà `1/65+1/64-1/63-1/62 \ne 0`

`-> x+66=0`

`-> x=-66`

a: =>2^x=2^4+16=32

=>x=5

b: Sửa đề: \(\dfrac{x+1}{65}+\dfrac{x+2}{64}=\dfrac{x+3}{63}+\dfrac{x+4}{62}\)

=>\(\left(\dfrac{x+1}{65}+1\right)+\left(\dfrac{x+2}{64}+1\right)=\left(\dfrac{x+3}{63}+1\right)+\left(\dfrac{x+4}{62}+1\right)\)

=>x+66=0

=>x=-66

53 + (124 - x) = 87

        (124 - x) = 87 - 53

        (124 - x) = 34

                    x = 124 - 34

                    x = 90

12.x - 64 = 2⁵

12.x - 64 = 32

12.x        = 32 + 64

12.x        = 96

     x        = 96 : 12

     x        = 8

1. ( x-2)² = 81

( x-2)² = 9²

=>x-2=9

x=9+2

x=11

a) Ta có: \(\left(x-1\right)^{x+2}-\left(x-1\right)^{x+4}=0\)

\(\Leftrightarrow\left(x-1\right)^x\cdot\left(x-1\right)^2-\left(x-1\right)^x\cdot\left(x-1\right)^4=0\)

\(\Leftrightarrow\left(x-1\right)^{x+2}\cdot\left[1-\left(x-1\right)^2\right]=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x-1=0\\x-1=1\\x-1=-1\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=1\\x=2\\x=0\end{matrix}\right.\)

b) Ta có: \(\dfrac{1}{4}\cdot\dfrac{2}{6}\cdot\dfrac{3}{8}\cdot\dfrac{4}{10}\cdot\dfrac{5}{15}\cdot...\cdot\dfrac{30}{62}\cdot\dfrac{31}{64}=2x\)

\(\Leftrightarrow2x=\dfrac{1}{64}\)

hay \(x=\dfrac{1}{128}\)

1/

$(x-1)^{x+10}=(x-1)^{x+8}$

$\Rightarrow (x-1)^{x+10}-(x-1)^{x+8}=0$

$\Rightarrow (x-1)^{x+8}(x^2-1)=0$

$\Rightarrow (x-1)^{x+8}=0$ hoặc $x^2-1=0$

Nếu $(x-1)^{x+8}=0\Rightarrow x-1=0\Rightarrow x=1$

Nếu $x^2-1=0\Rightarrow x^2=1=1^2=(-1)^2\Rightarrow x=1$ hoặc $x=-1$

Vậy $x=1$ hoặc $x=-1$

2/

$1^3+2^3+3^3+...+10^3=(x+1)^2$

Ta có công thức quen thuộc:

$1^3+2^3+...+n^3=(1+2+...+n)^2=\frac{[n(n+1)]^2}{4}$

Bạn có thể xem cm tại đây:

https://diendantoanhoc.org/topic/81694-t%C3%ADnh-t%E1%BB%95ng-s-13-23-33-n3/

Khi đó:

$1^3+2^3+...+10^3=(x+1)^2$

$\Rightarrow \frac{[10(10+1)]^2}{4}=(x+1)^2$

$\Rightarrow 3025=(x+1)^2$

$\Rightarrow x+1=55$ hoặc $x+1=-55$

$\Rightarrow x=54$ hoặc $x=-56$

a, ĐKXĐ:\(x\ge1\)

\(\sqrt{x-1}=3\\ \Rightarrow x-1=9\\ \Rightarrow x=10\)

\(b,x^2-64=0\\ \Rightarrow\left(x-8\right)\left(x+8\right)=0\\ \Rightarrow\left[{}\begin{matrix}x=8\\x=-8\end{matrix}\right.\\ c,x^2+16=25\\ \Rightarrow x^2=9\\ \Rightarrow\left[{}\begin{matrix}x=-3\\x=3\end{matrix}\right.\\ d,ĐKXĐ:x\ge0\\ \left|\sqrt{x}-3\right|+3=9\\ \Rightarrow\left|\sqrt{x}-3\right|=6\\ \Rightarrow\left[{}\begin{matrix}\sqrt{x}-3=-6\\x-3=6\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}\sqrt{x}=-3\left(vô.lí\right)\\x=9\left(tm\right)\end{matrix}\right.\)

(x - 5)² = 16

=> (x - 5)² = 4²

=> \(\orbr{\begin{cases}x-5=4\\x-5=-4\end{cases}}\)

=> \(\orbr{\begin{cases}x=9\\x=1\end{cases}}\)

(2x - 1)³ = -64

=> (2x - 1)³ = -4³

=> 2x - 1 = -4

=> 2x = -4 + 1

=> 2x = -3

=> x = -3/2

( x - 5)² = 16

=> (x - 5)² = 4²

=> \(\orbr{\begin{cases}x-5=4\\x-5=-4\end{cases}}\)

=> \(\orbr{\begin{cases}x=9\\x=1\end{cases}}\)