
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



(2x + y)2 - (2x - 3)2 = (2x + y - 2x + 3)(2x + y + 2x - 3) = (y + 3)(4x + y - 3)
\(\left(2x+y\right)^2-4x^2+12x-9\)
\(=\left(2x+y\right)^2-\left(2x-3\right)^2\)
\(=\left(2x+y-2x+3\right)\left(2x+y+2x-3\right)\)
\(=\left(y+3\right)\left(4x+y-3\right)\)

\(a,=4x^2+3xy-y^2+4xy-4x^2=7xy-y^2\\ b,=x^2-9-x^3+3x+x^2-3=-x^3+2x^2+3x-12\\ c,=-2x^2+12x-18+5x^2+4x-1=3x^2+16x-19\\ d,=8x^3+1-3x^3+6x^2=5x^3+6x^2+1\\ e,=\left(3x^2+4x+15x+20\right):\left(3x+4\right)\\ =\left(3x+4\right)\left(x+5\right):\left(3x+4\right)\\ =x+5\\ f,=\left(x^3+4x^2-3x+3x^2+12x-9+3x+3\right):\left(x^2+4x-3\right)\\ =\left[\left(x^2+4x-3\right)\left(x+3\right)+3x+3\right]:\left(x^2+4x-3\right)\\ =x+3\left(dư.3x+3\right)\)

Ta có : \(B\text{=}4x^2-12x+9\)
\(B\text{=}\left(2x-3\right)^2\)
Với \(x\text{=}\dfrac{1}{2}\)
\(\Rightarrow B\text{=}\left(2.\dfrac{1}{2}-3\right)^2\)
\(B\text{=}\left(-2\right)^2\text{=}4\)
Ta có : \(A\text{=}5\left(x+3\right)\left(x-3\right)+\left(2x+3\right)^2+\left(x-6\right)^2\)
\(A\text{=}5\left(x^2-9\right)+\left(2x+3\right)^2+\left(x-6\right)^2\)
\(A\text{=}5x^2-45+4x^2+12x+9+x^2-12x+36\)
\(A\text{=}10x^2\)
Với \(x\text{=}-\dfrac{1}{5}\)
\(\Rightarrow A\text{=}10.\left(-\dfrac{1}{5}\right)^2\text{=}\dfrac{2}{5}\)
B = 4x² - 12x + 9
= (2x - 3)²
Tại x = 1/2 ta có:
B = (2.1/2 - 3)²
= (-2)²
= 4
-------------------
A = 5(x + 3)(x - 3) + (2x + 3)² + (x - 6)²
= 5x² - 45 + 4x² + 12x + 9 + x² - 12x + 36
= 10x²
Tại x = 1/5 ta có:
A = 10.(1/5)²
= 2/5

a: \(x^2+4x+4=x^2+2\cdot x\cdot2+2^2=\left(x+2\right)^2\)
b: \(4x^2-4x+1=\left(2x\right)^2-2\cdot2x\cdot1+1^2=\left(2x-1\right)^2\)
c: \(2x-1-x^2\)
\(=-\left(x^2-2x+1\right)=-\left(x-1\right)^2\)
d: \(x^2+x+\dfrac{1}{4}=x^2+2\cdot x\cdot\dfrac{1}{2}+\left(\dfrac{1}{2}\right)^2=\left(x+\dfrac{1}{2}\right)^2\)
e: \(9-x^2=3^2-x^2=\left(3-x\right)\left(3+x\right)\)
g: \(\left(x+5\right)^2-4x^2=\left(x+5+2x\right)\left(x+5-2x\right)\)
\(=\left(5-x\right)\left(5+3x\right)\)
h: \(\left(x+1\right)^2-\left(2x-1\right)^2\)
\(=\left(x+1+2x-1\right)\left(x+1-2x+1\right)\)
\(=3x\left(-x+2\right)\)
i: \(=x^2y^2-4xy+4-3\)
\(=\left(xy-2\right)^2-3=\left(xy-2-\sqrt{3}\right)\left(xy-2+\sqrt{3}\right)\)
k: \(=y^2-\left(x-1\right)^2\)
\(=\left(y-x+1\right)\left(y+x-1\right)\)
l: \(=x^3+3\cdot x^2\cdot2+3\cdot x\cdot2^2+2^3=\left(x+2\right)^3\)
m: \(=\left(2x\right)^3-3\cdot\left(2x\right)^2\cdot y+3\cdot2x\cdot y^2-y^3=\left(2x-y\right)^3\)

1: \(\Leftrightarrow\left(x-3\right)\left(x+3\right)-\left(x-3\right)\left(5x+2\right)=0\)
\(\Leftrightarrow\left(x-3\right)\left(-4x+1\right)=0\)
hay \(x\in\left\{3;\dfrac{1}{4}\right\}\)
2: \(\Leftrightarrow\left(x-1\right)\left(x^2+x+1\right)-\left(x-1\right)\left(x^2-2x+16\right)=0\)
\(\Leftrightarrow\left(x-1\right)\left(x^2+x+1-x^2+2x-16\right)=0\)
\(\Leftrightarrow\left(x-1\right)\left(3x-15\right)=0\)
hay \(x\in\left\{1;5\right\}\)
3: \(\Leftrightarrow\left(x-1\right)\left(4x^2-1\right)=0\)
\(\Leftrightarrow\left(x-1\right)\left(2x-1\right)\left(2x+1\right)=0\)
hay \(x\in\left\{1;\dfrac{1}{2};-\dfrac{1}{2}\right\}\)
4: \(\Leftrightarrow x^2\left(x+4\right)-9\left(x+4\right)=0\)
\(\Leftrightarrow\left(x+4\right)\left(x-3\right)\left(x+3\right)=0\)
hay \(x\in\left\{-4;3;-3\right\}\)
5: \(\Leftrightarrow\left[{}\begin{matrix}3x+5=x-1\\3x+5=1-x\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}2x=-6\\4x=-4\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-3\\x=-1\end{matrix}\right.\)
6: \(\Leftrightarrow\left(6x+3\right)^2-\left(2x-10\right)^2=0\)
\(\Leftrightarrow\left(6x+3-2x+10\right)\left(6x+3+2x-10\right)=0\)
\(\Leftrightarrow\left(4x+13\right)\left(8x-7\right)=0\)
hay \(x\in\left\{-\dfrac{13}{4};\dfrac{7}{8}\right\}\)
1.
\(\Leftrightarrow\left(x-3\right)\left(x+3\right)=\left(x-3\right)\left(5x-2\right)\)
\(\Leftrightarrow x+3=5x-2\)
\(\Leftrightarrow4x=5\Leftrightarrow x=\dfrac{5}{4}\)
2.
\(\Leftrightarrow\left(x-1\right)\left(x^2+x+1\right)=\left(x-1\right)\left(x^2-2x+16\right)\)
\(\Leftrightarrow x^2+x+1=x^2-2x+16\)
\(\Leftrightarrow3x=15\Leftrightarrow x=5\)
3.
\(\Leftrightarrow4x^2\left(x-1\right)-\left(x-1\right)=0\)
\(\Leftrightarrow\left(x-1\right)\left(4x^2-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=1\\x=\dfrac{1}{2};x=-\dfrac{1}{2}\end{matrix}\right.\)

c: \(\left(2x+3\right)^2+\left(2x-3\right)^2-\left(2x+3\right)\left(2x-3\right)\)
\(=4x^2+12x+9+4x^2-12x+9-\left(4x^2-9\right)\)
\(=8x^2+18-4x^2+9=4x^2+27\)
d: \(\left(x-1\right)\cdot\left(x^2+x+1\right)-\left(2x+3\right)\left(4x^2-6x+9\right)\)
\(=\left(x-1\right)\left(x^2+x\cdot1+1^2\right)-\left(2x+3\right)\left[\left(2x\right)^2-2x\cdot3+3^2\right]\)
\(=x^3-1-8x^3-27=-7x^3-28\)
e: \(\left(x+1\right)^3-\left(x-1\right)^3-6x^2\)
\(=x^3+3x^2+3x+1-6x^2-\left(x^3-3x^2+3x-1\right)\)
\(=x^3-3x^2+3x+1-x^3+3x^2-3x+1\)
=2

\(a,=9x^2+12x+4-18x-4+10x^2=19x^2-6x\\ b,=8x^3-27-8x^3-36x^2-54x-27=-36x^2-54x-54\)
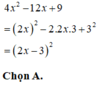
=(2x+1)^2-2(2x-3)(2x+1)+(4x^2-12x+9)
=(2x+1)^2-2(2x-3)(2x+1)+(2x-3)^2
=[(2x+1)-(2x-3)]^2
=(2x+1-2x+3)^2
=4^2=16
\(\left(2x+1\right)^2-2\left(2x-3\right)\left(2x+1\right)+4x^2-12x+9\)=\(=\left(2x+1\right)^2-2\left(2x+1\right)\left(2x-3\right)+\left(2x\right)^2-2.2x.3+3^2\)(ta thấy có dạng hằng đẳng thức \(A^2-2AB+B^2\))
\(=\left(\left(2x+1\right)-\left(2x-3\right)\right)^2\)
\(=\left(2x+1-2x+3\right)^2\)
\(=4^2\)=16