Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔOAI và ΔOBI có
OA=OB
\(\widehat{AOI}=\widehat{BOI}\)
OI chung
Do đó: ΔOAI=ΔOBI
\(a,\left\{{}\begin{matrix}OA=OB\\\widehat{AOI}=\widehat{BOI}\\OI\text{ chung}\end{matrix}\right.\Rightarrow\Delta AOI=\Delta BOI\left(c.g.c\right)\\ b,\text{Gọi }AB\cap OI=\left\{H\right\}\\ \left\{{}\begin{matrix}OA=OB\\\widehat{AOI}=\widehat{BOI}\\OH\text{ chung}\end{matrix}\right.\Rightarrow\Delta AOH=\Delta BOH\left(c.g.c\right)\\ \Rightarrow\widehat{AHO}=\widehat{BHO}\\ \text{Mà }\widehat{AHO}+\widehat{BHO}=180^0\\ \Rightarrow\widehat{AHO}=\widehat{BHO}=90^0\\ \Rightarrow OI\bot AB\)

a) xét ΔAOI,ΔBOIΔAOI,ΔBOI có :
OA = OB ( GT )
OI cạnh chung
AOIˆAOI^ = BOIˆBOI^ ( vì Oz phân giác xOyˆxOy^ )
⇒ΔAOI=ΔBOI(c.g.c)⇒ΔAOI=ΔBOI(c.g.c)
b )
gọi H là giao điểm AB , OI
xét ΔOAH,ΔOBHΔOAH,ΔOBH có
OH chung
AOHˆAOH^ = BOHˆBOH^ ( OI phân giác xOyˆxOy^ )
OA = OB ( GT )
⇒ΔOAH=ΔBOH(c.g.c)⇒ΔOAH=ΔBOH(c.g.c)
ta có : AHOˆAHO^ = BHOˆBHO^ ( 2 góc tương ứng )
mà AOHˆAOH^ + BHOˆBHO^ = 180o ( 2 góc kề bù )
⇒AOHˆ⇒AOH^ = BHOˆBHO^ = 180O2180O2 = 90o
⇒AB⊥OI⇒AB⊥OI tại H
link mình nha

a/ xét \(\Delta AOI;\Delta BOI\) có :
\(\hept{\begin{cases}OA=OB\\\widehat{O1}=\widehat{O2}\\IOchung\end{cases}}\)
\(\Leftrightarrow\Delta AOI=\Delta BOI\left(c-g-c\right)\)
b, gọi H là giao điểm của AB ; OI
Xét \(\Delta OAH;\Delta OBH\) có :
\(\hept{\begin{cases}OA=OB\\\widehat{O1}=\widehat{O2}\\AHchung\end{cases}}\)
\(\Leftrightarrow\Delta OAH=\Delta OBH\left(c-g-c\right)\)
\(\Leftrightarrow\widehat{H1}=\widehat{H2}\)
Mà \(\widehat{H1}+\widehat{H2}=180^0\)
\(\Leftrightarrow\widehat{H1}=\widehat{H2}=\frac{180^0}{2}=90^0\)
\(\Leftrightarrow OI\perp AB\left(đpcm\right)\)

Hình bạn tự vẽ nha
Xét \(\Delta AIO\) và \(\Delta BIO\) có:
OI chung
\(\widehat{AOI} = \widehat{BOI}\) (Oz là tia phân giác của \(\widehat{xOy}\) (gt))
OA = OB (gt)
\(\Rightarrow\)\(\Delta AIO = \Delta BIO\) (cgc)
b) Vì \(\Delta AIO = \Delta BIO\) (cmt)
\(\Rightarrow IB=IA\) (2 cạnh tương ứng)
mà OA = OB (gt)
\(\Rightarrow OI\) là đường trung trực của AB
hay \(AB \perp OI\)
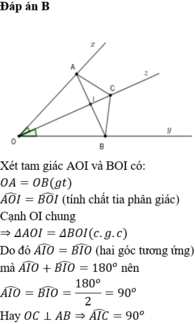
a: Xét ΔOAI và ΔOBI có
OA=OB
\(\widehat{AOI}=\widehat{BOI}\)
OI chung
Do đó: ΔOAI=ΔOBI