\(\frac{2}{5}.\frac{1}{x}+\frac{1}{x}.2+\frac{2}{5}=0,5\)

\(\Rightarrow\frac{2}{5x}+\frac{2}{x}+\frac{2}{5}=\frac{1}{2}\)

\(\Rightarrow2.\left(\frac{1}{5x}+\frac{1}{x}+\frac{1}{5}\right)=\frac{1}{2}\)

\(\Rightarrow\frac{1}{5x}+\frac{5}{5x}+\frac{x}{5x}=\frac{1}{2}:2=\frac{1}{4}\)

\(\Rightarrow\frac{1+5+x}{5x}=\frac{1}{4}\)

\(\Rightarrow4.\left(1+5+x\right)=5x\)

\(\Rightarrow4+20+4x=5x\)

\(\Rightarrow24+4x=5x\)

\(\Rightarrow5x-4x=24\)

\(\Rightarrow x=24\)

Trả lời

2/5.1/x+1/x.2+2/5=0,5

1/x.(2/5+2)+2/5   =1/2

1/x.12/5+2/5        =1/2

1/x.12/5               =1/2-2/5

1/x.12/5               =1/10

1/x                       =1/10:12/5

1/x                       =1/24.

Hình như mk làm sai !

b)\(\left(x-8\right)\left(x-2\right)=0\Leftrightarrow\orbr{\begin{cases}x-8=0\\x-2=0\end{cases}}\Leftrightarrow\orbr{\begin{cases}x=8\\x=2\end{cases}}\)

c) \(\left(x+1\right)+\left(x+2\right)+...+\left(x+10\right)=9x+200\)

\(\Leftrightarrow\left(x+x+...+x\right)+\left(1+2+...+10\right)=9x+200\) (10 số hạng x)

\(\Leftrightarrow10x+55=9x+200\Leftrightarrow x+55=200\)

\(\Leftrightarrow x=145\)

các bạn ơi giúp mik ý đầu tiên đi

\(c,\overline{735a2b}⋮̸2;⋮5\Rightarrow b=5\\ \Rightarrow\overline{735a25}⋮9\\ \Rightarrow7+3+5+a+2+5⋮9\\ \Rightarrow22+a⋮9\\ \Rightarrow a=5\\ \Rightarrow\overline{735a2b}=735525\\ b,\overline{5a27b}⋮2;⋮5\Rightarrow b=0\\ \Rightarrow\overline{5a270}⋮9\\ \Rightarrow5+a+2+7+0⋮9\\ \Rightarrow14+a⋮9\\ \Rightarrow a=4\\ \Rightarrow\overline{5a27b}=54270\)

c) \(735525\)
d) \(54270\)

Xét : \(\frac{a}{5}=\frac{12}{144}\Leftrightarrow a=\frac{5}{12}\)

Xét : \(\frac{b}{3}=\frac{12}{144}\Leftrightarrow b=\frac{1}{4}\)

Xét ; \(\frac{c}{8}=\frac{12}{144}\Leftrightarrow c=\frac{2}{3}\)

Ta có 

\(\hept{\begin{cases}\frac{a}{5}=\frac{12}{144}\\\frac{b}{3}=\frac{12}{144}\\\frac{c}{8}=\frac{12}{144}\end{cases}}\Leftrightarrow\hept{\begin{cases}a=5.12:144=\frac{5}{12}\\b=3.12:144=\frac{1}{4}\\c=8.12:144=\frac{2}{3}\end{cases}}\)

vậy a=5/12 và b=1/4 và c=2/3

tính  

28.112-28.12+31

=28.(112-12)+31

=28.100+31

=2800+31

=2831

tim x  

42 + 2(x-7) =128

2(x-7)=86

x-7=43

x=50

Tính nhanh : 

 a, 28.112-28.12+31

=28.(112-12)+31

=28.100+31

=2800 + 31

=2831

tìm x : 

a, 42+2.(x-7)=128

2.(x+7)=128-42

2.(x+7)=86

x+7=86:2

x+7=43

x=43-7

x=36

Vậy x=36

`5/2 -3(1/3-x)=1/4-7x`

`=> 5/2 - 1 + 3x=1/4 -7x`

`=>3x+7x= 1/4 - 5/2 +1`

`=> 10x= 1/4 - 10/4 +4/4`

`=>10x= -5/4`

`=>x=-5/4 :10`

`=>x=-5/4 xx1/10`

`=>x= -5/40=-1/8`

=>5/2-3+3x=1/4-7x

=>10x=1/4-5/2+3=3/4

=>x=3/40

\(\dfrac{-1}{9}.\dfrac{3}{5}+\dfrac{-1}{4}.\dfrac{-4}{5}+\dfrac{1}{9}.\dfrac{2}{5}\)

\(\text{=}\dfrac{-1}{15}+\dfrac{1}{5}+\dfrac{2}{45}\)

\(\text{=}\dfrac{8}{45}\)

Áp dụng tính chất đổi dấu và giao hoán của phép nhân phân số, ta có:

\(\dfrac{-1}{9}.\dfrac{3}{5}+\dfrac{-1}{4}.\dfrac{-4}{5}+\dfrac{1}{9}.\dfrac{2}{5}=\dfrac{1}{5}.\dfrac{-3}{9}+\dfrac{1}{5}.\dfrac{4}{4}+\dfrac{1}{5}.\dfrac{2}{9}\)

                                           \(=\dfrac{1}{5}\left(-\dfrac{3}{9}+1+\dfrac{2}{9}\right)\)

                                           \(=\dfrac{1}{5}\left(-\dfrac{3}{9}+\dfrac{9}{9}+\dfrac{2}{9}\right)\)

                                           \(=\dfrac{1}{5}.\dfrac{8}{9}\)

                                           \(=\dfrac{8}{45}\)

Câu 26 trang 89 Sách Bài Tập (SBT) Toán Lớp 6 tập 2

So sánh hai góc ở hình 10.

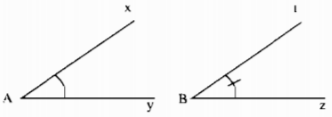
Hướng dẫn:

Cách 1: Đo riêng từng góc rồi so sánh hai số đó

Cách 2: Vẽ lại hai góc lên giấy trong. Đặt chồng hai góc sao cho đỉnh trùng nhau, một cạnh trùng nhau, hai cạnh còn lại của hai góc nằm cùng phía đối với cạnh trùng nhau rồi vận dụng kiến thức bài 5 để kết luận.

Giải

Dùng thước đo độ để đo hai góc ở hình 10 và so sánh.

Tính tổng số đo hai góc trên hình 10.

Hướng dẫn:

Cách 1: Đo riêng từng góc rồi cộng hai số đo.

Cách 2: Vẽ hai góc ở vị trí kề nhau rồi đo góc tổng.

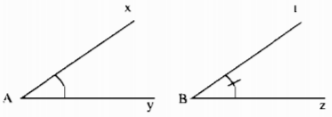
Giải

Sử dụng thước đo độ sau đó cộng số đo hai góc.

a) Vẽ góc  có đỉnh là M trên giấy cứng. Cắt ra ta được một mẫu hình.

b) Đóng hai chiếc đinh vào hai điểm A và B cách nhau 2,5 cm. Đưa mẫu hình vào khe hở giữa hai chiếc đinh sao cho một cạnh sát A, một cạnh sát B. Khi đó đỉnh M của góc ở vị trí \(M_1\). Đặt mẫu hình nhiều lần để được nhiều vị trí \(M_1,M_2,M_3\).. khác nhau của đỉnh M. Vậy ta có:
                                        \(\widehat{AM_1B}=\widehat{AM_2B}=\widehat{AM_3B}=...=40^o\)

Đánh dấu khoảng 10 vị trí khác nhau của đỉnh M và dự đoán quỹ đạo của đỉnh M (hình 11)

Giải

b) Quỹ đạo của điểm M được gọi là "cung chứa góc \(40^o\)

Bài 29 tự làm,có trong sách mà bạn

Bài 26 trang 89 Toán 6

So sánh hai góc ở hình 10.

Hướng dẫn: Cách 1: Đo riêng từng góc rồi so sánh hai số đó

Cách 2: Vẽ lại hai góc lên giấy trong. Đặt chồng hai góc sao cho đỉnh trùng nhau, một cạnh trùng nhau, hai cạnh còn lại của hai góc nằm cùng phía đối với cạnh trùng nhau rồi vận dụng kiến thức bài 5 để kết luận.

Giải: Dùng thước đo độ để đo hai góc ở hình 10 và so sánh.

Bài 27 trang 89

Tính tổng số đo hai góc trên hình 10.

Hướng dẫn:

Cách 1: Đo riêng từng góc rồi cộng hai số đo.

Cách 2: Vẽ hai góc ở vị trí kề nhau rồi đo góc tổng.

Giải: Sử dụng thước đo độ sau đó cộng số đo hai góc.

Bài 28 Toán 6

a) Vẽ góc  có đỉnh là M trên giấy cứng. Cắt ra ta được một mẫu hình.

b) Đóng hai chiếc đinh vào hai điểm A và B cách nhau 2,5 cm. Đưa mẫu hình vào khe hở giữa hai chiếc đinh sao cho một cạnh sát A, một cạnh sát B. Khi đó đỉnh M của góc ở vị trí M1M1. Đặt mẫu hình nhiều lần để được nhiều vị trí M1,M2,M3M1,M2,M3, … khác nhau của đỉnh M. Vậy ta có:

ˆAM1B=ˆAM2B=ˆAM3B=…=400AM1B^=AM2B^=AM3B^=…=400

Đánh dấu khoảng 10 vị trí khác nhau của đỉnh M và dự đoán quỹ đạo của đỉnh M (hình 11)

HD: b) Quỹ đạo của điểm M được gọi là “cung chứa góc 400400.

29a) Ta có hình vẽ

b) Vì ˆARNARN^ và ˆSRNSRN^ kề bù nên:

ˆARN+ˆSRN=180OARN^+SRN^=180O

Thay ˆSRN=130OSRN^=130O ta có:

ˆARN+130O=180OARN^+130O=180O

⇒ˆARN=180O–130O=50O⇒ARN^=180O–130O=50O

Vì ˆARMARM^ và ˆMRSMRS^ kề bù nên:

ˆARM+ˆMRS=180OARM^+MRS^=180O

Thay ˆARM=130OARM^=130O ta có:

130O+ˆMRS=180O130O+MRS^=180O

⇒ˆMRS=180O–130O=50O⇒MRS^=180O–130O=50O

Vì hai tia RN và RM nằm trên cùng môt nửa mặt phẳng bờ chứa tia RA

ˆARN=50O;ˆARM=130OARN^=50O;ARM^=130O suy ra ˆARN<ˆARMARN^<ARM^

Nên tia RN nằm giữa hai tia RA và RM

⇒ˆARN+ˆMRN=ˆARM⇒ARN^+MRN^=ARM^. Thay ˆARN=50O;ˆARM=130OARN^=50O;ARM^=130O ta có:

50O+ˆMRN=130O50O+MRN^=130O

⇒ˆMRN=130O–50O=80O

1)(5.5-5).5:5.5=100

2)(5.5-5).5.5:5=100

3)5.(5.5-5).5:5=100

k cho mik nha

bn ơi 5 chữ số 5 nha ko phải là 6 chữ số 5