\(=\frac{5\cdot2^{20}\cdot3^{11}+7\cdot2^{29}\cdot3^{18}}{5\cdot2^{30}\cdot3^{18}-2^{29}\cdot3^{20}}=\frac{2^{20}\cdot3^{11}\left(5+7\cdot2^9\cdot3^7\right)}{2^{29}\cdot3^{18}\left(5\cdot2-3^2\right)}=\frac{5+7\cdot2^9\cdot3^7}{2^9\cdot3^7\cdot1}\)

...

\(\Leftrightarrow a=15\cdot8+4\cdot9-35=121\)

a) Sắp xếp lại mẫu số liệu theo thứ tự không giảm, ta được:

2; 2; 5; 7; 10; 10; 13; 15; 19

+) Vì cỡ mẫu là \(n = 9\), là số lẻ, nên giá trị tứ phân vị thứ hai là \({Q_2} = 10\)

+) Tứ phân vị thứ nhất là trung vị của mẫu: 2; 2; 5; 7.

Do đó \({Q_1} = \frac{1}{2}(2 + 5) = 3,5\)

+) Tứ phân vị thứ nhất là trung vị của mẫu: 10; 13; 15; 19.

Do đó \({Q_3} = \frac{1}{2}(13 + 15) = 14\)

b) Sắp xếp lại mẫu số liệu theo thứ tự không giảm, ta được:

1; 2; 5; 5; 9; 10; 10; 15; 15; 19

+) Vì cỡ mẫu là \(n = 10\), là số chẵn, nên giá trị tứ phân vị thứ hai là \({Q_2} = \frac{1}{2}(9 + 10) = 9,5\)

+) Tứ phân vị thứ nhất là trung vị của mẫu: 1; 2; 5; 5; 9.

Do đó \({Q_1} = 5\)

+) Tứ phân vị thứ nhất là trung vị của mẫu: 10; 10; 15; 15; 19.

Do đó \({Q_3} = 15\)

\(\Leftrightarrow4^{3x}+4^x\ge\left(2^{3x}+12.2^x+6.2^{2x}+8\right)+2^x+2\)

\(\Leftrightarrow\left(4^x\right)^3+4^x\ge\left(2^x+2\right)^3+\left(2^x+2\right)\)

\(\Leftrightarrow f\left(4^x\right)\ge f\left(2^x+2\right)\)

Với \(f\left(t\right)=t^3+t,t>0;f'\left(t\right)=3t^2+1>0\) với mọi t

Do đó hàm số \(f\left(t\right)\) đồng biến trên R

Suy ra \(4^x\ge2^x+2\Leftrightarrow\left(2^x\right)^2-2^x-2\ge0\Leftrightarrow\left(2^x+1\right)\left(2^x-1\right)\ge0\)

                              \(\Leftrightarrow2^x-1\ge0\Leftrightarrow x\ge0\)

Vậy tập nghiệm bất phương trình là S = [0;+\(\infty\))

Chọn A.

Lập bảng tần số- tần suất:

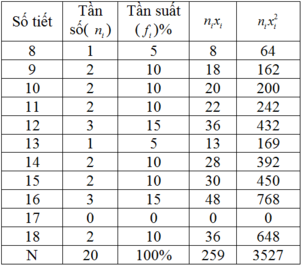
Phương sai của dãy số liệu trên là: