
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{2}=\dfrac{y}{3}=\dfrac{z}{5}=\dfrac{x-2y+3z}{2-2\cdot3+3\cdot5}=\dfrac{33}{11}=3\)
Do đó: x=6; y=9; z=15

Do ( x+6) ^2 > = 0 với mọi x
/ y - 7 / > = 0 với mọi x
=> x = -6 , y = 7
=> x + y = 1
Vì \(\hept{\begin{cases}\left(x+6\right)^2\ge0\forall x\\\left|y-7\right|\ge0\forall y\end{cases}}\)
\(\Rightarrow\left(x+6\right)^2+\left|y-7\right|\ge0\forall x;y\)
Dấu "=" xảy ra <=> \(\hept{\begin{cases}\left(x+6\right)^2=0\\\left|y-7\right|=0\end{cases}\Rightarrow\hept{\begin{cases}x+6=0\\y-7=0\end{cases}\Rightarrow}\hept{\begin{cases}x=-6\\y=7\end{cases}}}\)
\(\Rightarrow x+y=-6+7=1\)

Đặt \(\frac{x}{3}=-\frac{y}{7}=k\Rightarrow x=3k;y=-7k\)
Ta có: xy=-189
=> 3k.(-7k)=-189
=> -21k2=-189
=> k2=(-189):(-21)
=> k2=9=32=(-3)2
=> k=3 hoặc k=-3
TH1: k=3 => x=3k=3.3=9
=> y=-7k=-7.3=-21
Mà x < y nên loại TH1.
TH2: k=-3 => x=3k=3.(-3)=-9
=> y=-7k=-7.(-3)=21
Vì x < y mà -9 < 21 nên chọn
Vậy x=-9.

x + 2 x y + y = 7
x + 3 x y = 7
nếu y = 1 thì x =4
nếu y = 0 thì x = 7
nếu y = 2 thì x = 1

1) Ta có: |x+3| \(\ge\)0; |2x+y-4| \(\ge\)0
\(\Rightarrow\) |x + 3| + |2x + y - 4| \(\ge\) 0
Dấu = xảy ra khi x+3=0 và 2x+y-4 = 0 \(\Rightarrow\)x=-3; y=10
1) |x + 3| + |2x + y - 4| = 0
\(\Leftrightarrow\hept{\begin{cases}x+3=0\\2x+y-4=0\end{cases}}\Leftrightarrow\hept{\begin{cases}x=-3\\-6+y-4=0\end{cases}}\Leftrightarrow\hept{\begin{cases}x=-3\\y=10\end{cases}}\)

x : 2 = y : 5 hay \(\frac{x}{2}=\frac{y}{5}\)
Ta có :
\(\frac{x}{2}=\frac{y}{5}=\frac{x+y}{2+5}=\frac{-21}{7}=-3\)
\(\Rightarrow x=3.2=6\) và \(y=3.5=15\)

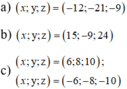
ta có:
\(\frac{7}{x}=\frac{y}{21}=\frac{-42}{54}\)
=> \(\frac{7}{x}=\frac{-42}{54}\Rightarrow x=\frac{7\cdot54}{\left(-42\right)}=-9\)
=> \(\frac{y}{21}=\frac{-42}{54}\Rightarrow y=\frac{21\cdot\left(-42\right)}{54}=-16\frac{1}{3}\)