a) \(A=\frac{1}{3}+\frac{1}{3^2}+\frac{1}{3^3}+...+\frac{1}{3^n}\)

\(3A=1+\frac{1}{3}+\frac{1}{3^2}+...+\frac{1}{3^{n-1}}\)

\(3A-A=\left(1+\frac{1}{3}+\frac{1}{3^2}+...+\frac{1}{3^{n-1}}\right)-\left(\frac{1}{3}+\frac{1}{3^2}+\frac{1}{3^3}+...+\frac{1}{3^n}\right)\)

\(2A=1-\frac{1}{3^n}\)

\(A=\frac{1-\frac{1}{3^n}}{2}\)

b) Gọi số cần tìm là ab (a khác 0; a,b là các chữ số)

Ta có: ab.75 = x² \(\left(x\ne0\right)\)

=> ab.3.5² = x²

Để ab.75 là 1 số chính phương thì ab = 3.k² \(\left(k\ne0\right)\)

Lại có: 9 < ab < 100 => 9 < 3.k² < 100

=> 3 < k² < 34

Mà k² là số chính phương nên \(k^2\in\left\{4;9;16;25\right\}\)

\(\Rightarrow ab\in\left\{12;27;48;75\right\}\)

Vậy số cần tim là 12; 27; 48; 75

c) Đặt \(B=\frac{1}{3}+\frac{2}{3^2}+\frac{3}{3^3}+...+\frac{101}{3^{101}}\)

\(3B=1+\frac{2}{3}+\frac{3}{3^2}+...+\frac{101}{3^{100}}\)

\(3B-B=\left(1+\frac{2}{3}+\frac{3}{3^2}+...+\frac{101}{3^{100}}\right)-\left(\frac{1}{3}+\frac{2}{3^2}+\frac{3}{3^3}+...+\frac{101}{3^{101}}\right)\)

\(2B=1+\frac{1}{3}+\frac{1}{3^2}+...+\frac{1}{3^{100}}-\frac{101}{3^{101}}\)

\(6B=3+1+\frac{1}{3}+...+\frac{1}{3^{99}}-\frac{101}{3^{100}}\)

\(6B-2B=\left(3+1+\frac{1}{3}+...+\frac{1}{3^{99}}-\frac{101}{3^{100}}\right)-\left(1+\frac{1}{3}+\frac{1}{3^2}+...+\frac{1}{3^{100}}-\frac{101}{3^{101}}\right)\)

\(4B=3-\frac{101}{3^{100}}-\frac{1}{3^{100}}+\frac{101}{3^{101}}\)

\(4B=3-\frac{303}{3^{101}}-\frac{3}{3^{101}}+\frac{101}{3^{101}}\)

\(4B=3-\frac{205}{3^{101}}< 3\)

\(\Rightarrow B< \frac{3}{4}\)

Minh bo sung cau c la tong do be hon 3/4

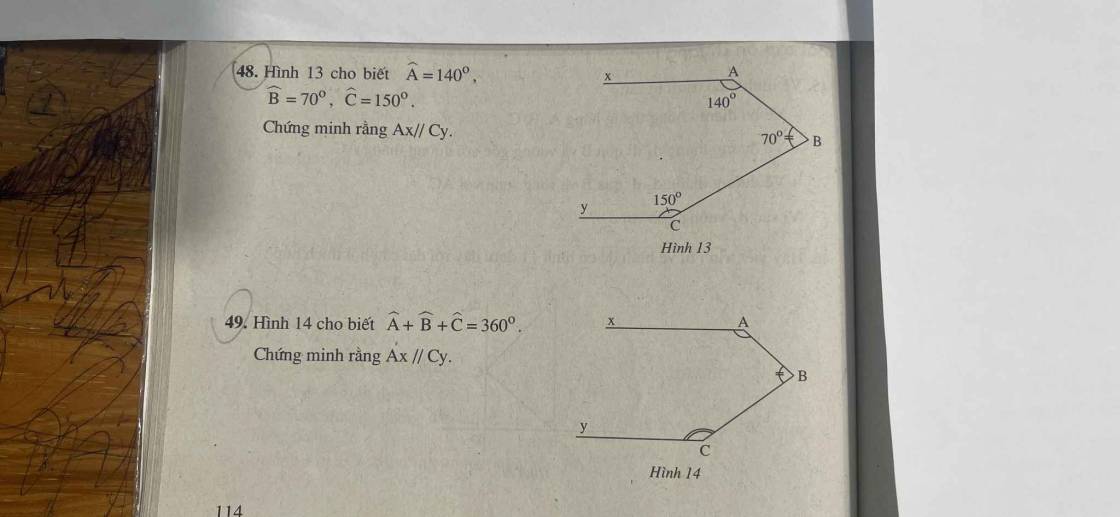
48.

Gọi O là giao của Ax với BC. Xét tg ABO có

\(\widehat{OAB}=\widehat{xAO}-\widehat{xAB}=180^o-140^o=40^o\)

\(\widehat{OBA}=\widehat{CBO}-\widehat{ABC}=180^o-70^o=110^o\)

\(\Rightarrow\widehat{AOB}=180^o-\left(\widehat{OAB}+\widehat{OBA}\right)=180^o-\left(40^o+110^o\right)=30^o\)

\(\Rightarrow\widehat{yCB}+\widehat{AOB}=150^o+30^o=180^o\) hai góc này nằm ở vị trí 2 góc trong cùng phía và bù nhau => Ax//Cy

49.

Nối A với C. Xét tg ABC có

\(\widehat{BAC}+\widehat{BCA}+\widehat{B}=180^o\)

Ta có

\(\widehat{A}+\widehat{B}+\widehat{C}=360^o\)

\(\Rightarrow\widehat{xAC}+\widehat{BAC}+\widehat{B}+\widehat{yCA}+\widehat{BCA}=360^o\)

\(\Rightarrow\left(\widehat{xAC}+\widehat{yCA}\right)+\left(\widehat{BAC}+\widehat{BCA}+\widehat{B}\right)=360^o\)

\(\Rightarrow\widehat{xAC}+\widehat{yCA}=360^o-\left(\widehat{BAC}+\widehat{BCA}+\widehat{B}\right)=\)

\(=360^o-180^o=180^o\)

Hai góc \(\widehat{xAC}\) và \(\widehat{yCA}\) ở vị trí 2 góc trong cùng phía và bù nhau

=> Ax//Cy

(2x+1)³=8000

(2x+1)³=20³

=> 2x+1=20

     2x    =20-1=19

      x     =19/2

cac bn giup mk nhe

\(M=\left(5x-3y+3xy+x^2y^2\right)-\left(\dfrac{1}{2}x+2xy-y+4x^2y^2\right)\)

\(=5x-3y+3xy+x^2y^2-\dfrac{1}{2}x-2xy+y-4x^2y^2\)

\(=\left(5x-\dfrac{1}{2}x\right)+\left(y-3y\right)+\left(3xy-2xy\right)+\left(x^2y^2-4x^2y^2\right)\) \(=4,5x-2y+xy-3x^2y^2\)

Thay \(x=1;y=-\dfrac{1}{2}\) vào ta có:

\(4,5x-2y+xy-3x^2y^2\)

\(=4,5.1-2.\left(-\dfrac{1}{2}\right)+1.\left(-\dfrac{1}{2}\right)-3.1^2.\left(-\dfrac{1}{2}\right)^2\)

\(=4,5+1-\dfrac{1}{2}-\dfrac{3}{4}\) \(=\dfrac{17}{4}\)