
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



\(A=1\cdot2+2\cdot3+...+151\cdot152\)
\(=1\left(1+1\right)+2\left(1+2\right)+...+151\left(1+151\right)\)
\(=\left(1+2+3+...+151\right)+\left(1^2+2^2+...+151^2\right)\)
\(=\dfrac{151\left(151+1\right)}{2}+\dfrac{151\left(151+1\right)\left(2\cdot151+1\right)}{6}\)
\(=151\cdot76+\dfrac{151\cdot152\cdot303}{6}\)
\(=151\cdot76+151\cdot7676=1170552\)
\(C=2\cdot4+4\cdot6+...+2024\cdot2026\)
\(=2\cdot2\left(1\cdot2+2\cdot3+...+1012\cdot1013\right)\)
\(=4\left[1\left(1+1\right)+2\left(1+2\right)+...+1012\left(1+1012\right)\right]\)
\(=4\left[\left(1+2+...+1012\right)+\left(1^2+2^2+...+1012^2\right)\right]\)
\(=4\left[1012\cdot\dfrac{1013}{2}+\dfrac{1012\left(1012+1\right)\left(2\cdot1012+1\right)}{6}\right]\)
\(=4\left[506\cdot1013+345990150\right]\)
\(=1386010912\)
\(M=1^2+2^2+...+2024^2\)
\(=\dfrac{2024\left(2024+1\right)\cdot\left(2\cdot2024+1\right)}{6}\)
\(=2024\cdot2025\cdot\dfrac{4049}{6}\)
=2765871900
\(N=1^3+2^3+...+100^3\)
\(=\left(1+2+3+...+100\right)^2\)
\(=\left[\dfrac{100\left(100+1\right)}{2}\right]^2\)
\(=\left[50\cdot101\right]^2=5050^2\)
\(Q=1^3+2^3+...+2024^3\)
\(=\left(1+2+3+...+2024\right)^2\)
\(=\left[\dfrac{2024\left(2024+1\right)}{2}\right]^2\)
\(=\left[1012\left(2024+1\right)\right]^2\)
\(=2049300^2\)

kết quả đó chắc chắn là đúng mà . làm sao sai được
Mình ko biết mới hỏi chứ! Tại thi violimpic trả lời nó bảo sai nên mới biết.

Cho A=1/1.2 + 1/2.3 + + 1/ 3.4+...+1/49.50 ; B = 1.2+2.3+3.4+4.5+5.6+...+49.50
Tính 50 mủ 2 A – B/17


3A=1.2.3+2.3.3+3.4.3+4.5.3+.....+9.10.3
3A=1.2.(3-0)+2.3.(4-1)+3.4.(5-2)+4.5.(6-3)+.....+9.10.(11-8)
3A=1.2.3-1.2.0+2.3.4-1.2.3+.....+9.10.11-9.10.8
3A=9.10.11
A=(9.10.11):3
A=330
CHẮC CHẮN 100% LÀ ĐÚNG

\(\text{Ta có: A = 1.2+2.3+3.4+4.5+...+99.100 }\)
=> 3A = 3.(1.2+2.3+3.4+4.5+...+99.100)
=> 3A = 1.2.(3 - 0) +2.3.(4 - 1) + 3.4.(5-2) + ........ + 99.100.(101 - 98)
=> 3A = 1.2.3 - 1.2.3 + 2.3.4 - 2.3.4 + .......... + 99.100.101
=> 3A = 99.100.101
\(\Rightarrow A=\frac{99.100.101}{3}=333300\)
k mình nếu đúng OK

A = 1.2 + 2.3 + 3.4 + ... + 99.100 + 100.101
⇒ 3A = 1.2.3 + 2.3.3 + 3.4.3 + ... + 99.100.3 + 100.101.3
= 1.2.3 + 2.3.(4 - 1) + 3.4.(5 - 2) + ... + 99.100.(101 - 98) + 100.101.(102 - 99)
= 1.2.3 - 1.2.3 + 2.3.4 - 2.3.4 + 3.4.5 + ... - 98.99.100 + 99.100.101 - 99.100.101 + 100.101.102
= 100.101.102
= 1030200
⇒ A = 1030200 : 3
= 343400

Áp dụng công thức ta có :
\(A=1.2+2.3+3.4+...+99.100=\frac{99.100.101}{3}=333300\)

A=1.2+2.3+3.4+4.5+...+2014.2015
=>3A=1.2.3+2.3.3+3.4.3+4.5.3+...+2014.2015.3
=1.2.(3-0)+2.3.(4-1)+3.4.(5-2)+4.5.(6-3)+...+2014.2015.(2016-2013)
=1.2.3-0.1.2+2.3.4-1.2.3+3.4.5-2.3.4+4.5.6-3.4.5+...+2014.2015.2016-2013.2014.2015
=(1.2.3-1.2.3)+(2.3.4-2.3.4)+(3.4.5-3.4.5)+(4.5.6-4.5.6)+...+(2013.2014.2015-2013.2014.2015)+0.1.2+2014.2015.2016
=0+2014.2015.2016
=>A=\(\frac{2014.2015.2016}{3}\)
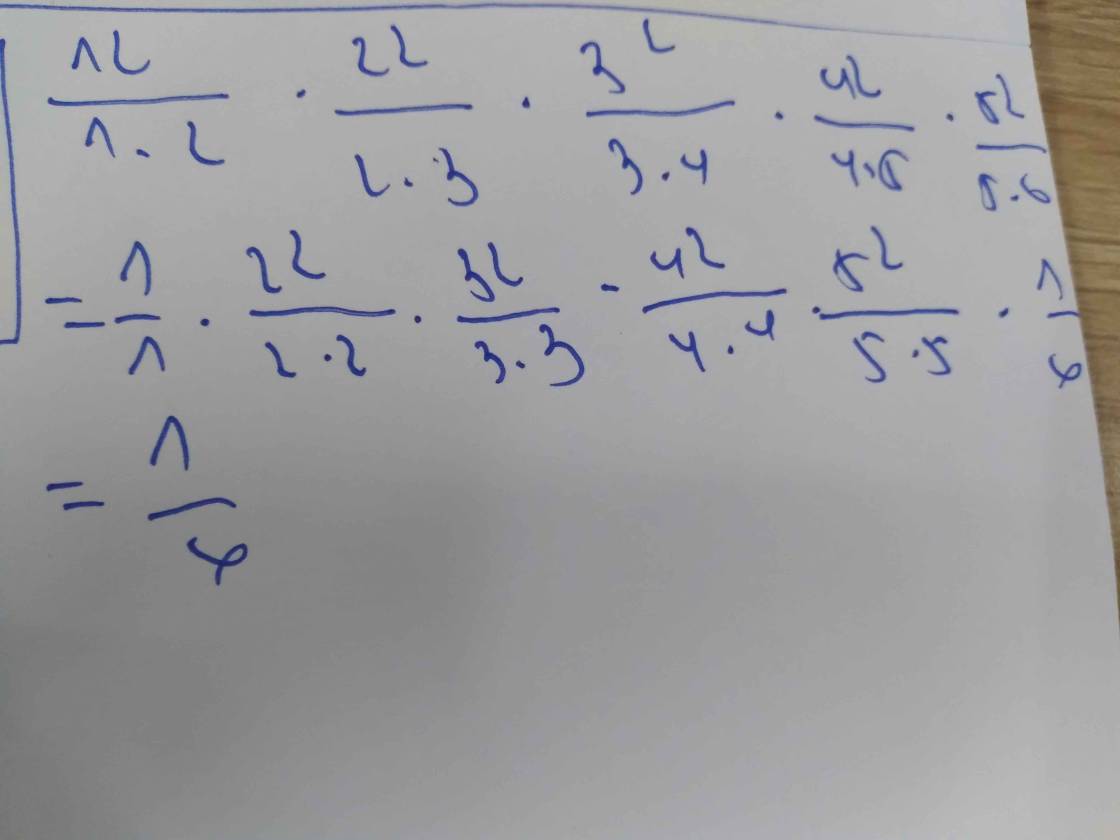
xem trên mạng
Giúp đi