Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tham khảo:
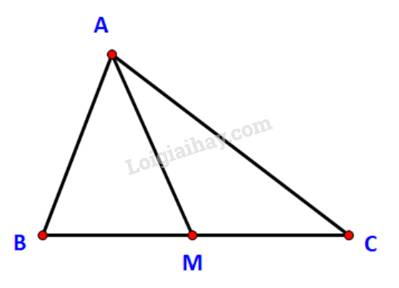
a) Ta có: \(\widehat {AMB} + \widehat {AMC} = {180^o}\)
\( \Rightarrow \cos \widehat {AMB} = - \cos \widehat {AMC}\)
Hay \(\cos \widehat {AMB} + \cos \widehat {AMC} = 0\)
b) Áp dụng định lí cos trong tam giác AMB ta có:
\(\begin{array}{l}A{B^2} = M{A^2} + M{B^2} - 2MA.MB\;\cos \widehat {AMB}\\ \Leftrightarrow M{A^2} + M{B^2} - A{B^2} = 2MA.MB\;\cos \widehat {AMB}\;\;(1)\end{array}\)
Tương tự, Áp dụng định lí cos trong tam giác AMB ta được:
\(\begin{array}{l}A{C^2} = M{A^2} + M{C^2} - 2MA.MC\;\cos \widehat {AMC}\\ \Leftrightarrow M{A^2} + M{C^2} - A{C^2} = 2MA.MC\;\cos \widehat {AMC}\;\;(2)\end{array}\)
c) Từ (1), suy ra \(M{A^2} = A{B^2} - M{B^2} + 2MA.MB\;\cos \widehat {AMB}\;\)
Từ (2), suy ra \(M{A^2} = A{C^2} - M{C^2} + 2MA.MC\;\cos \widehat {AMC}\;\)
Cộng vế với vế ta được:
\(2M{A^2} = \left( {A{B^2} - M{B^2} + 2MA.MB\;\cos \widehat {AMB}} \right)\; + \left( {A{C^2} - M{C^2} + 2MA.MC\;\cos \widehat {AMC}} \right)\;\)
\( \Leftrightarrow 2M{A^2} = A{B^2} + A{C^2} - M{B^2} - M{C^2} + 2MA.MB\;\cos \widehat {AMB} + 2MA.MC\;\cos \widehat {AMC}\)
Mà: \(MB = MC = \frac{{BC}}{2}\) (do AM là trung tuyến)
\( \Rightarrow 2M{A^2} = A{B^2} + A{C^2} - {\left( {\frac{{BC}}{2}} \right)^2} - {\left( {\frac{{BC}}{2}} \right)^2} + 2MA.MB\;\cos \widehat {AMB} + 2MA.MB\;\cos \widehat {AMC}\)
\( \Leftrightarrow 2M{A^2} = A{B^2} + A{C^2} - 2.{\left( {\frac{{BC}}{2}} \right)^2} + 2MA.MB\;\left( {\cos \widehat {AMB} + \;\cos \widehat {AMC}} \right)\)
\( \Leftrightarrow 2M{A^2} = A{B^2} + A{C^2} - {\frac{{BC}}{2}^2}\)
\(\begin{array}{l} \Leftrightarrow M{A^2} = \frac{{A{B^2} + A{C^2} - {{\frac{{BC}}{2}}^2}}}{2}\\ \Leftrightarrow M{A^2} = \frac{{2\left( {A{B^2} + A{C^2}} \right) - B{C^2}}}{4}\end{array}\) (đpcm)
Cách 2:
Theo ý a, ta có: \(\cos \widehat {AMC} = - \cos \widehat {AMB}\)
Từ đẳng thức (1): suy ra \(\cos \widehat {AMB} = \frac{{M{A^2} + M{B^2} - A{B^2}}}{{2.MA.MB}}\)
\( \Rightarrow \cos \widehat {AMC} = - \cos \widehat {AMB} = - \frac{{M{A^2} + M{B^2} - A{B^2}}}{{2.MA.MB}}\)
Thế \(\cos \widehat {AMC}\)vào biểu thức (2), ta được:
\(M{A^2} + M{C^2} - A{C^2} = 2MA.MC.\left( { - \frac{{M{A^2} + M{B^2} - A{B^2}}}{{2.MA.MB}}} \right)\)
Lại có: \(MB = MC = \frac{{BC}}{2}\) (do AM là trung tuyến)
\(\begin{array}{l} \Rightarrow M{A^2} + {\left( {\frac{{BC}}{2}} \right)^2} - A{C^2} = 2MA.MB.\left( { - \frac{{M{A^2} + M{B^2} - A{B^2}}}{{2.MA.MB}}} \right)\\ \Leftrightarrow M{A^2} + {\left( {\frac{{BC}}{2}} \right)^2} - A{C^2} = - \left( {M{A^2} + M{B^2} - A{B^2}} \right)\\ \Leftrightarrow M{A^2} + {\left( {\frac{{BC}}{2}} \right)^2} - A{C^2} + M{A^2} + {\left( {\frac{{BC}}{2}} \right)^2} - A{B^2} = 0\\ \Leftrightarrow 2M{A^2} - A{B^2} - A{C^2} + {\frac{{BC}}{2}^2} = 0\\ \Leftrightarrow 2M{A^2} = A{B^2} + A{C^2} - {\frac{{BC}}{2}^2}\\ \Leftrightarrow M{A^2} = \frac{{A{B^2} + A{C^2} - {{\frac{{BC}}{2}}^2}}}{2}\\ \Leftrightarrow M{A^2} = \frac{{2\left( {A{B^2} + A{C^2}} \right) - B{C^2}}}{4}\end{array}\)

A. \({a^2} = {b^2} + {c^2} + \sqrt 2 ab.\) (Loại)
Vì: Theo định lí cos ta có: \({a^2} = {b^2} + {c^2} - 2bc.\cos A\)
Không đủ dữ kiện để suy ra \({a^2} = {b^2} + {c^2} + \sqrt 2 ab.\)
B. \(\frac{b}{{\sin A}} = \frac{a}{{\sin B}}\) (Loại)
Theo định lí sin, ta có: \(\frac{a}{{\sin A}} = \frac{b}{{\sin B}} \nRightarrow \frac{b}{{\sin A}} = \frac{a}{{\sin B}}\)
C. \(\sin B = \frac{{ - \sqrt 2 }}{2}\)(sai vì theo câu a, \(\sin B = \frac{{\sqrt 2 }}{2}\))
D. \({b^2} = {c^2} + {a^2} - 2ca\cos {135^o}.\)
Theo định lý cos ta có:
\({b^2} = {c^2} + {a^2} - 2ca.\cos B\) (*)
Mà \(\widehat B = {135^o} \Rightarrow \cos B = \cos {135^o}\).
Thay vào (*) ta được: \({b^2} = {c^2} + {a^2} - 2ca\;\cos {135^o}\)
=> D đúng.
Chọn D

Ta có: \(\alpha = {90^o} \Rightarrow \cos \alpha = \cos {90^o} = 0\)
\( \Rightarrow {b^2} + {c^2} - 2bc.\cos \alpha = {b^2} + {c^2}\)
Mà tam giác ABC có \(\alpha = {90^o}\) nên: \({a^2} = {b^2} + {c^2}\)
Do đó \({a^2} = {b^2} + {c^2} - 2bc.\cos \alpha \) (đpcm)

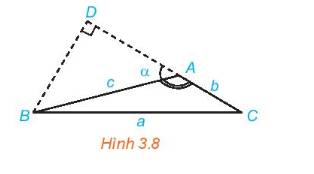
a) Xét tam giác BDC vuông tại D, theo định lý Pythagore ta có:
\({a^2} = B{D^2} + D{C^2}\) (1)
b) Xét tam giác vuông BDA ta có:
\(\left\{ \begin{array}{l}B{A^2} = B{D^2} + D{A^2} \Rightarrow B{D^2} = B{A^2} - D{A^2} = {c^2} - D{A^2}\\\cos \alpha = \frac{{DA}}{c} \Rightarrow DA = c.\cos \alpha \end{array} \right.\)
Lại có: DC = DA + AC = DA + b Thế vào (1)
\( \Rightarrow {a^2} = \left( {{c^2} - D{A^2}} \right) + {\left( {DA + b} \right)^2}\) (2)
c) Xét tam giác vuông BDA ta có:
\(\cos \alpha = \frac{{DA}}{c} \Rightarrow DA = c.\cos \alpha \)
Mà \(\cos \alpha = - \cos A\) (do góc \(\alpha \) và góc A bù nhau)
\( \Rightarrow DA = - \,\,c.\cos A\)
d) Thế \(DA = - \,\,c.\cos A\) vào (2) ta được:
\(\begin{array}{l}{a^2} = \left[ {{c^2} - {{\left( { - \,\,c.\cos A} \right)}^2}} \right] + {\left( { - \,\,c.\cos A + b} \right)^2}\\ \Leftrightarrow {a^2} = \left( {{c^2} - \,\,{c^2}.{{\cos }^2}A} \right) + \left( {{c^2}.{{\cos }^2}A - \,2b\,c.\cos A + {b^2}} \right)\\ \Leftrightarrow {a^2} = {c^2} - \,\,{c^2}.{\cos ^2}A + {c^2}.{\cos ^2}A - \,2b\,c.\cos A + {b^2}\\ \Leftrightarrow {a^2} = {b^2} + {c^2} - \,2b\,c.\cos A\end{array}\) (đpcm)
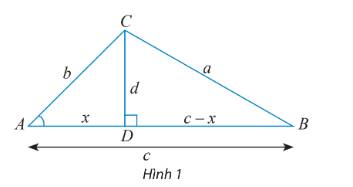
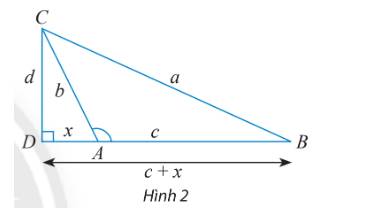
a) ? = x vì \(\cos A = \frac{{AD}}{{AC}} = \frac{x}{b} \Rightarrow ? = x.\)
b) Xét tam giác vuông BCD, ta có: \({a^2} = {d^2} + {(c + x)^2} = {d^2} + {x^2} + {c^2} + 2xc\) (1)
Xét tam giác vuông ACD, ta có: \({b^2} = {d^2} + {x^2} \Rightarrow {d^2} = {b^2} - {x^2}\) (2)
\(\cos A = - \cos \widehat {DAC} = - \frac{x}{b} \Rightarrow x = - b\cos A.\) (3)
Thay (2) và (3) vào (1), ta có: \({a^2} = {b^2} + {c^2} - 2bc\cos A\)
c) Ta có: \({a^2} = {b^2} + {c^2} - 2bc\cos A\)
Mà \(\widehat A = {90^o} \Rightarrow \cos A = \cos {90^o} = 0.\)
\( \Rightarrow {a^2} = {b^2} + {c^2}\)