Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a, Ta có \(\sqrt{25-16}=\sqrt{9}=3\)
\(\sqrt{25}-\sqrt{16}=5-4=1\)
Do 3 > 1 nên \(\sqrt{25-16}>\sqrt{25}-\sqrt{16}\)
a) căn 25 - 16 > căn 25 - căn 16
b)Với nên đều xác định
Để so sánh và ta quy về so sánh và .
+) .
+)
.
Do nên
Do
(đpcm)
Vậy .

b) Ta sẽ chứng minh bằng biến đổi tương đương :)
Ta có : \(\sqrt{a}-\sqrt{b}< \sqrt{a-b}\)
\(\Leftrightarrow a+b-2\sqrt{ab}< a-b\)
\(\Leftrightarrow2b-2\sqrt{ab}< 0\)
\(\Leftrightarrow2\sqrt{b}\left(\sqrt{b}-\sqrt{a}\right)< 0\) (1)
Vì a>b nên \(b-a< 0\Leftrightarrow\left(\sqrt{b}-\sqrt{a}\right)\left(\sqrt{b}+\sqrt{a}\right)< 0\Leftrightarrow\sqrt{b}-\sqrt{a}< 0\) (vì \(\sqrt{a}+\sqrt{b}>0\))
Lại có \(\sqrt{b}>0\) \(\Rightarrow2\sqrt{b}\left(\sqrt{b}-\sqrt{a}\right)< 0\) đúng.
Vì bđt cuối đúng nên bđt ban đầu được chứng minh
\(\sqrt{25-16}=\sqrt{9}=3\)
\(\sqrt{25}-\sqrt{16}=5-4=1\)
\(\sqrt{25-16}>\sqrt{25}-\sqrt{16}\)

a) Ta có:
+)√25+9=√34+)25+9=34.
+)√25+√9=√52+√32=5+3+)25+9=52+32=5+3
=8=√82=√64=8=82=64.
Vì 34<6434<64 nên √34<√6434<64
Vậy √25+9<√25+√925+9<25+9
b) Với a>0,b>0a>0,b>0, ta có
+)(√a+b)2=a+b+)(a+b)2=a+b.
+)(√a+√b)2=(√a)2+2√a.√b+(√b)2+)(a+b)2=(a)2+2a.b+(b)2
=a+2√ab+b=a+2ab+b
=(a+b)+2√ab=(a+b)+2ab.
Vì a>0, b>0a>0, b>0 nên √ab>0⇔2√ab>0ab>0⇔2ab>0
⇔(a+b)+2√ab>a+b⇔(a+b)+2ab>a+b
⇔(√a+√b)2>(√a+b)2⇔(a+b)2>(a+b)2
⇔√a+√b>√a+b⇔a+b>a+b (đpcm)
a, Ta có : \(\sqrt{25+9}=\sqrt{34}\)
\(\sqrt{25}+\sqrt{9}=5+3=8=\sqrt{64}\)
mà 34 < 64 hay \(\sqrt{25+9}< \sqrt{25}+\sqrt{9}\)
b, \(\sqrt{a+b}< \sqrt{a}+\sqrt{b}\)
bình phương 2 vế ta được : \(a+b< a+2\sqrt{ab}+b\)
\(\Leftrightarrow2\sqrt{ab}>0\)vì \(a;b>0\)nên đẳng thức này luôn đúng )
Vậy ta có đpcm

a) \(\sqrt{36-25}=\sqrt{11}\)
\(\sqrt{36}-\sqrt{25}=6-5=1\)
Suy ra \(\sqrt{36-25}>\sqrt{36}-\sqrt{25}\)
a,\(\sqrt{36-25}=-1\)
\(\sqrt{36}-\sqrt{25}=1\)
Vậy: \(\sqrt{36-25}< \sqrt{36}-\sqrt{25}\)

a) Tính √25 + √9 rồi so sánh kết quả với .
Trả lời: < √25 + √9.
b) Ta có: = a + b và
=
+ 2√a.√b +
= a + b + 2√a.√b.
Vì a > 0, b > 0 nên √a.√b > 0.
Do đó < √a + √b
a) Tính √25 + √9 rồi so sánh kết quả với .
Trả lời: < √25 + √9.
b) Ta có: = a + b và
=
+ 2√a.√b +
= a + b + 2√a.√b.
Vì a > 0, b > 0 nên √a.√b > 0.
Do đó < √a + √b

So sánh:
\(a,\sqrt{25+9}\)và \(\sqrt{25}+\sqrt{9}\)
Ta có:
\(\sqrt{25+9}=\sqrt{34}< \sqrt{36}=6\) \(\left(1\right)\)
\(\sqrt{25}+\sqrt{9}=\sqrt{5^2}+\sqrt{3^2}=5+3=8\) \(\left(2\right)\)
Từ (1) và (2) \(\Rightarrow\sqrt{25+9}< \sqrt{25}+\sqrt{9}\)
\(b,\sqrt{25-16}\) và \(\sqrt{25}-\sqrt{16}\)
Tương tự:)

1) c/m \(a+b+c\ge\sqrt{ab}+\sqrt{bc}+\sqrt{ac}\)
áp dụng BĐT cô shi cho 2 số thực dương ta có:
\(a+b\ge2\sqrt{ab}\);\(b+c\ge2\sqrt{bc}\);\(a+c\ge2\sqrt{ac}\)
cộng vế vs vế:\(2\left(a+b+c\right)\ge2\left(\sqrt{ab}+\sqrt{bc}+\sqrt{ca}\right)\)
↔\(a+b+c\ge\sqrt{ab}+\sqrt{bc}+\sqrt{ca}\)
dấu = xảy ra khi a=b=c
vậy...
b)ta có:
\(\frac{1}{\sqrt{1}}>\frac{1}{\sqrt{2}}>\frac{1}{\sqrt{3}}>...>\frac{1}{\sqrt{25}}\)→\(A>\frac{1}{\sqrt{25}}+\frac{1}{\sqrt{25}}+...+\frac{1}{\sqrt{25}}\)(25 số hạng)
\(A>\frac{25}{\sqrt{25}}=\sqrt{25}=5\)
vậy.....

a) HD: Thực hiện phép khai căn rồi so sánh kết quả.
Trả lời: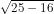 > √25 - √16;.
> √25 - √16;.
b) HD: Ta có thể chứng minh rằng √a <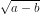 + √b.
+ √b.
Nhưng điều này suy ra từ kết quả bài tập 26.b) SGK nếu lưu ý rằng
√a = .
.
a) Ta có:
\(\sqrt{25-16}=\sqrt{9}=3\);
\(\sqrt{25}-\sqrt{16}=5-4=1\).
Vì 1 < 3 nên \(\sqrt{25}-\sqrt{16}< \sqrt{25-16}\).
b) Ta có:
\(\sqrt{a}=\sqrt{a-b+b}=\sqrt{(a-b)+b}\)
mà ta đã biết:
\(\sqrt{(a-b)+b}< \sqrt{a-b}+\sqrt{b}\)
\(\Leftrightarrow\sqrt{a}< \sqrt{a-b}+\sqrt{b}\)
\(\Leftrightarrow\sqrt{a}-\sqrt{b}< \sqrt{a-b}\)
Vậy \(\sqrt{a}-\sqrt{b}< \sqrt{a-b}\).