Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Số đường chéo của đa giác n cạnh là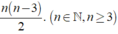
Số đường chéo của đa giác 14 cạnh là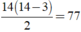 đường chéo
đường chéo

Số đường chéo của đa giác n cạnh là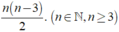
Số đường chéo của đa giác 14 cạnh là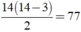 đường chéo
đường chéo

Gọi n là số cạnh của đa giác.
Ta có :
- Số đường chéo của đa giác là : n(n−3)2
Cái này dễ chứng minh thôi bn!
Từ mỗi đỉnh của hình n giác lồi ta vẽ được n - 1 đoạn thẳng nối đỉnh đó với n - 1 đỉnh còn lại, trong đó có 2 đoạn thẳng trùng với 2 cạnh của đa giác. Vậy qua mỗi đỉnh của hình n giác lồi vẽ được n - 3 đường chéo, hình n giác có n đỉnh nên vẽ được n(n - 3) đường chéo, trong đó mỗi đường chéo được tính 2 lần nên thực chất chỉ có n(n−3)2 đường chéo.
- Tổng số đo các góc trong đa giác : 180o.(n−2)
Còn số cạnh của đa giác thì tự đếm ra, nếu đề bài cho 1 số gt bắt tìm số cạnh thì dựa vào công thức tính đường chéo hay công thức tính số đo 1 góc đa giác đều (180o.(n−2)n.
Số đường chéo xuất phát từ mỗi đỉnh của đa giác n cạnh là n - 3.
__________________

Chọn 2 trong n đỉnh của đa giác ta lập được 1 cạnh hoặc đường chéo.(n>=3,n thuộc N*)
Số cạnh và đường chéo là C2n (đường).
⇒ Số đường chéo của đa giác n cạnh là C2n−n (đường).
Theo đề bài, số đường chéo gấp đôi số cạnh nên ta có phương trình:
C2n−n=2n⇔n!/2!(n−2)!=3n
⇔n(n−1)(n−2)!/2(n−2)!=3n
⇔n(n−1)=6n
⇔n^2−7n=0
⇔[n=7(tm) n=0(ktm)
Vậy đa giác cần tìm có 7 cạnh.

Số đường chéo của đa giác n cạnh là (n( n - 3 ))/2. ( n ∈ N, n ≥ 3 )
Theo giả thiết ta có (n( n - 3 ))/2 = n ⇔ n( n - 3 ) = 2n ⇔ n 2 - 3 n - 2 n = 0
⇔
n
2
-
5
n
=
0
⇔
n
(
n
-
5
)
=
0
⇔ 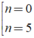
So sánh điều kiện ta có n = 5 thỏa mãn.
Chọn A

Số đường chéo đa giác có 7 cạnh là: 7. ( 7 − 3 ) 2 = 14
Công thức tổng quát tính số đường chéo đa giác: n . ( n − 3 ) 2

Hướng dẫn:
+ Số đo của một góc của đa giác đều n cạnh là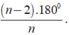
Khi đó số đo của một góc của đa giác đều 20 cạnh là:
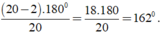
+ Số đường chéo của đa giác n cạnh là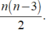
Khi đó số đường chéo của đa giác đều 20 cạnh là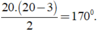

a) \(\frac{\left(24-3\right).24}{2}=252\)đường chéo
b) \(\left(n-3\right).n=340\)
\(n^2-3n=340\)
\(n^2-3n-340=0\)
\(n^2-20n+17n-340=0\)
\(n\left(n-20\right)+17\left(n-20\right)\)
\(\left(n+17\right)\left(n-20\right)=0\)
\(\Leftrightarrow\)\(\orbr{\begin{cases}n+17=0\\n-20=0\end{cases}}\)\(\Leftrightarrow\)\(\orbr{\begin{cases}n=-17\\n=20\end{cases}}\)
n = -17 ( loại )
n = 20 ( nhận )
Vậy n = 20 hay số cạnh của đa giác là 20
1 Đa giác có n cạnh có :
- Số đường chéo từ 1 đỉnh là : (n - 3)
- Số đỉnh là n
Do 1 đường chéo nối 2 đỉnh
=> 1 Đa giác có n cạnh có n(n - 3)/2 đường chéo
biết tổng số đường chéo là 170
=> n(n - 3)/2 = 170
=> n² - 3n - 340 = 0
∆ = (-3)² - 4.(-340) = 1369
=> √∆ = 37
=> n = ... (tự giải)